In the previous article, we learnt the technique of "how to multiply numbers with a series of 9’s". In this article, we shall learn the technique of "how to multiply numbers with a series of 1’s". So, we shall multiply the numbers with 1, 11, 111,..... etc.
I. Let us start with the vedic multiplication by 11
In this technique, we use "vertically and crosswise" vedic sutra. Take example of ab x uv, and apply the sutra as follows:
a b
u v
---------------------
a x u | av + ub | b x v
---------------------
(Here '|' is used just as separator)
Here we are splitting the answer in three parts as following:
a b
1 1
--------------------
a | a + b | b
--------------------
Example: Multiply 53 by 11
Here one point to consider is that we should write the answer from right to left. Because, in case, sum of the digits of multiplicand comes in 2 digits, we need to carry the ten's place digit to next (left side) calculation. You will notice it in next examples.
Example: Multiply 68 by 11
Step 1 : Last part of the answer is same as the last part of the multiplicand i.e. 8 (8 x 1). > 8
Step 2 : For middle part, sum the digits of multiplicand i.e. 6 + 8 = 14. We will not write '14' as the middle part. We write down '4' and digit '1' is carried over. > 4
Step 3 : First part is now, first digit of multiplicand i.e. 6. But we have one digit as carry from step 2, so we shall add this to first part. Now first part will become 6 + 1 = 7. > 7
Finally, answer is 748.
Some examples are given below:
54 x 11= 5 | 9 | 4 = 594
35 x 11= 3 | 8 | 5 = 385
81 x 11= 8 | 9 | 1 = 891
96 x 11= 9 | 15 | 6 = 10 | 5 | 6 = 1023 ( here '1' carry over)
88 x 11= 8 | 16 | 8 = 9 | 6 | 8 = 968 (again '1' carry over)
This technique is also applicable to numbers having more than 2 digits. You just need to take first and last digits of multiplicand as it is (as done in previous examples), and continue adding the adjacent two numbers for middle parts (more than one parts now).
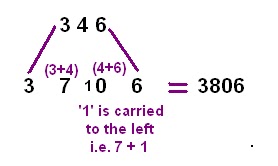
Example: Multiply 346 by 11
Following examples will help to understand more.
267 x 11 = 2 | 2+6 | 6+7 | 7
= 2 | 8 | 13 | 7
= 2 | 9 | 3 | 7
= 2937
2678 x 11 = 2 | 2+6 | 6+7 | 7+8 | 8
= 2 | 8 | 13 | 15 | 8
= 2 | 9 | 4 | 5 | 8
= 29458
26789 x 11 = 2 | 2+6 | 6+7 | 7+8 | 8+9 | 9
= 2 | 8 | 13 | 15 | 17 | 9
= 2 | 9 | 4 | 6 | 7 | 9
= 294679
II. Now, let us learn to multiply any number with 111.
In this, since multiplier is 3-digit number, so for middle part, we shall start by adding first two digits and then keep on adding next three ( and next three and so on) and then will end by adding the last two digits. First and last part will be same as described above. You will understand this with following examples.
Examples:
365 x 111 = 3 | 3+6 | 3+6+5 | 6+5 | 5
= 3 | 9 | 14 | 11 | 5
= 40515
3645 x 111 = 3 | 3+6 | 3+6+4 | 6+4+5 | 4+5 | 5
= 3 | 9 | 13 | 15 | 9 | 5
= 404595
567894 x 111 = 5 | 5+6 | 5+6+7 | 6+7+8 | 7+8+9 | 8+9+4 | 9+4 | 4
= 5 | 11 | 18 | 21 | 24 | 21 | 13 | 4
= 63036234
57 x 111 = 057 x 111
= 0 | 0+5 | 0+5+7 | 5+7 | 7
= 0 | 5 | 12 | 12 | 7
= 06327 = 6327
III. Similarly, we can multiple any number by 1111.
In this, since multiplier is 4-digit number, so for middle part, we shall start by adding first two digits, then first three digits and then keep on adding next four ( and next four and so on) and then will end by adding the last three digits, and then last two digits. First and last part will be same as described above. You will understand this with following examples.
Examples:
5678 x 1111 = 5 | 5+6 | 5+6+7 | 5+6+7+8 | 6+7+8 | 7+8 | 8
= 5 | 11 | 18 | 26 | 21 | 15 | 8
= 6308258
126453 x 1111 = 1 | 1+2 | 1+2+6 | 1+2+6+4 | 2+6+4+5 | 6+4+5+3 | 4+5+3 | 5+3 | 3
= 1 | 3 | 9 | 13 | 17 | 18 | 12 | 8 | 3
= 140489283
43 x 1111 = 0043 x 1111
= 0 | 0+0 | 0+0+4 | 0+0+4+3 | 0+4+3 | 4+3 | 3
= 0 | 0 | 4 | 7 | 7 | 7 | 3
= 47773
Using the same method, we can multiply any number by a series of 1’s. If you want to multiply a number by 11111 (irrespective of how big is the multiplicand), the only difference will be that we will add maximum five numbers at a time for middle part of answer(because there are five ones in 11111).
And remember the basic rule that we use in normal addition — carry over the digit to its left when you have a two-digit answer.
I. Let us start with the vedic multiplication by 11
In this technique, we use "vertically and crosswise" vedic sutra. Take example of ab x uv, and apply the sutra as follows:
a b
u v
---------------------
a x u | av + ub | b x v
---------------------
(Here '|' is used just as separator)
Here we are splitting the answer in three parts as following:
- vertically =(b x v)
- crosswise multiplication and add =(a x v) + (b x u)
- vertically =(a x u)
a b
1 1
--------------------
a | a + b | b
--------------------
Example: Multiply 53 by 11
Here one point to consider is that we should write the answer from right to left. Because, in case, sum of the digits of multiplicand comes in 2 digits, we need to carry the ten's place digit to next (left side) calculation. You will notice it in next examples.
Example: Multiply 68 by 11
Step 1 : Last part of the answer is same as the last part of the multiplicand i.e. 8 (8 x 1). > 8
Step 2 : For middle part, sum the digits of multiplicand i.e. 6 + 8 = 14. We will not write '14' as the middle part. We write down '4' and digit '1' is carried over. > 4
Step 3 : First part is now, first digit of multiplicand i.e. 6. But we have one digit as carry from step 2, so we shall add this to first part. Now first part will become 6 + 1 = 7. > 7
Finally, answer is 748.
Some examples are given below:
54 x 11= 5 | 9 | 4 = 594
35 x 11= 3 | 8 | 5 = 385
81 x 11= 8 | 9 | 1 = 891
96 x 11= 9 | 15 | 6 = 10 | 5 | 6 = 1023 ( here '1' carry over)
88 x 11= 8 | 16 | 8 = 9 | 6 | 8 = 968 (again '1' carry over)
This technique is also applicable to numbers having more than 2 digits. You just need to take first and last digits of multiplicand as it is (as done in previous examples), and continue adding the adjacent two numbers for middle parts (more than one parts now).
Example: Multiply 346 by 11
Following examples will help to understand more.
267 x 11 = 2 | 2+6 | 6+7 | 7
= 2 | 8 | 13 | 7
= 2 | 9 | 3 | 7
= 2937
2678 x 11 = 2 | 2+6 | 6+7 | 7+8 | 8
= 2 | 8 | 13 | 15 | 8
= 2 | 9 | 4 | 5 | 8
= 29458
26789 x 11 = 2 | 2+6 | 6+7 | 7+8 | 8+9 | 9
= 2 | 8 | 13 | 15 | 17 | 9
= 2 | 9 | 4 | 6 | 7 | 9
= 294679
II. Now, let us learn to multiply any number with 111.
In this, since multiplier is 3-digit number, so for middle part, we shall start by adding first two digits and then keep on adding next three ( and next three and so on) and then will end by adding the last two digits. First and last part will be same as described above. You will understand this with following examples.
Examples:
365 x 111 = 3 | 3+6 | 3+6+5 | 6+5 | 5
= 3 | 9 | 14 | 11 | 5
= 40515
3645 x 111 = 3 | 3+6 | 3+6+4 | 6+4+5 | 4+5 | 5
= 3 | 9 | 13 | 15 | 9 | 5
= 404595
567894 x 111 = 5 | 5+6 | 5+6+7 | 6+7+8 | 7+8+9 | 8+9+4 | 9+4 | 4
= 5 | 11 | 18 | 21 | 24 | 21 | 13 | 4
= 63036234
57 x 111 = 057 x 111
= 0 | 0+5 | 0+5+7 | 5+7 | 7
= 0 | 5 | 12 | 12 | 7
= 06327 = 6327
III. Similarly, we can multiple any number by 1111.
In this, since multiplier is 4-digit number, so for middle part, we shall start by adding first two digits, then first three digits and then keep on adding next four ( and next four and so on) and then will end by adding the last three digits, and then last two digits. First and last part will be same as described above. You will understand this with following examples.
Examples:
5678 x 1111 = 5 | 5+6 | 5+6+7 | 5+6+7+8 | 6+7+8 | 7+8 | 8
= 5 | 11 | 18 | 26 | 21 | 15 | 8
= 6308258
126453 x 1111 = 1 | 1+2 | 1+2+6 | 1+2+6+4 | 2+6+4+5 | 6+4+5+3 | 4+5+3 | 5+3 | 3
= 1 | 3 | 9 | 13 | 17 | 18 | 12 | 8 | 3
= 140489283
43 x 1111 = 0043 x 1111
= 0 | 0+0 | 0+0+4 | 0+0+4+3 | 0+4+3 | 4+3 | 3
= 0 | 0 | 4 | 7 | 7 | 7 | 3
= 47773
Using the same method, we can multiply any number by a series of 1’s. If you want to multiply a number by 11111 (irrespective of how big is the multiplicand), the only difference will be that we will add maximum five numbers at a time for middle part of answer(because there are five ones in 11111).
And remember the basic rule that we use in normal addition — carry over the digit to its left when you have a two-digit answer.