Vedic Math - Multiplication of any Numbers

In the previous article, we have discussed few cases of Multiplication with "vertically and crosswise" sutra. In this article, we shall learn the remaining cases.

E. Multiplying three digit by three digit numbers
For example: abc x pqr

Multiply:
1) vertically                                              (a x p)
2) crosswise in both directions and add    (a x q) + (b x p)
3) crosswise in both directions and add    (a x r) + (b x q) + (c x p)
4) crosswise in both directions and add    (b x r) + (c x q)
5) vertically                                              (c x r)

Step2 and Step4 are same as we did in the previous sections i.e. multiplying crosswise with two columns at a time. But in Step3, we multiply crosswise using the outer columns, then multiply vertically in the middle column and add these numbers.

Example: 456 x 258
  4            5           6      
  2            5           8
--------------------------------------
  8 | 20+10 | 32+25+12 | 40+30 | 48
= 8 | 30 | 69 | 70 | 48
= 8 | 30 | 69 | (70+4) | 8
= 8 | 30 | 69 | 74 | 8
= 8 | 30 | (69+7) | 4 | 8
= 8 | 30 | 76 | 4 | 8
= 8 | (30+7) | 6 | 4 | 8
= 8 | 37 | 6 | 4 | 8
= (8+3) | 7 | 6 | 4 | 8
= 11 | 7 | 6 | 4 | 8
Hence 456 x 258 = 117648

The Algebraic Expression is:
Let the two numbers be (ax² + bx + c) and (dx² + ex + f).
Note that x=10

Now the product is
= (ax² + bx + c) (dx² + ex + f)
= ad.x⁴ + bd.x³ + cd.x² + ae. x³ + be.x² + ce.x + af.x² + bf.x + cf
= ad.x⁴ + (bd + ae). x³ + (cd + be + af).x² + (ce + bf)x + cf

The Vertically and Crosswise formula can also be Extended into 2 by 2 method. See the following example:
 123 × 132

We can split the numbers up into 12 | 3 and 13 | 2 , treating 12 and 13 as if they are single figures:
 12      3
 13      2
-------------
156 | 63 | 6
= (156+6) | 3 | 6
= 162 | 3 | 6
= 16236

F. Multiplying four digit by three digit numbers
For abcd x pqr

Multiply:
1) vertically                                              (a x p)
2) crosswise in both directions and add    (a x q) + (b x p)
3) crosswise in both directions and add    (a x r) + (b x q) + (c x p)
4) crosswise in both directions and add    (b x r) + (c x q) + (d x p)
5) crosswise in both directions and add    (c x r) + (d x q)
6) vertically                                             (d x r)

Example: 4562 x 258
  4          5            6           2      
             2            5           8
----------------------------------------------
  8 | 20+10 | 32+25+12 | 40+30+4 | 48+10 | 16
= 8 | 30 | 69 | 74 | 58 | 16
= 8 | 30 | 69 | 74 | (58+1) | 6
= 8 | 30 | 69 | 74 | 59 | 6
= 8 | 30 | 69 | (74+5) | 9 | 6
= 8 | 30 | 69 | 79 | 9 | 6
= 8 | 30 | (69+7) | 9 | 9 | 6
= 8 | 30 | 76 | 9 | 9 | 6
= 8 | (30+7) | 6 | 9 | 9 | 6
= 8 | 37 | 6 | 9 | 9 | 6
= (8+3) | 7 | 6 | 9 | 9 | 6
= 11 | 7 | 6 | 9 | 9 | 6
 4562 x 258 = 1176996

I hope this would help you in quick multiplication. If you have any doubt, you can welcome to post your queries.

If you like the article, you may contribute by:

• Posting your comments which will add value to the article contents
• Posting the article link on Social Media using the Social Media Bookmark bar
• Connecting with 'VedantaTree' on Facebook (https://www.facebook.com/VedantaTree)

Vedic Math - Multiplication of any numbers

In this article, we shall discuss the Vedic Math sutra "vertically and crosswise". This is the General Formula which is applicable to all the cases of multiplication. You will found this method very useful in division also that we shall discuss later. In the previous sutras, you subtracted crosswise; now you will multiply crosswise.

A. Multiplication of two digit numbers
For ab x uv

The numbers are written from left to right.
Now multiply:
1) vertically                                              (a x u)
2) crosswise in both directions and add    (a x v) + (b x u)
3) vertically                                              (b x v)

The answer has the form:   au | av + bu | bv

Following is the example of two-digit multiplication will make this clear:
12 x 23
 1         2
 2         3
--------------
2 | 3 + 4 | 6
= 2 | 7 | 6
= 276

The previous examples involved no carry figures, so let us consider this case in the next example.
64 x 93
 6          4
 9          3
-----------------
54 | 18 + 36 | 12
=54 | 54 | 12
=54 | (54 + 1) | 2         (Carry over the 1)
=54 | 55 | 2
=(54 + 5) | 5 | 2          (Carry over the 5)
=59 | 5 | 2
64 x 93 =5952

The Algebraic Explaination is:
Let the two 2 digit numbers be (ax+b) and (ux+v). Note that x = 10. Now consider the product
(ax + b) (ux + v)
= au. x² + avx + bux + b.v
= au. x² + (av + bu)x + b.v
The first term i. e. the coefficient of  x² is got by vertical multiplication of a and u
The middle term i. e. the coefficient of x is obtained by the cross-wise multiplication of a and v and of b and u and the addition of the two products
The independent term is arrived at by vertical multiplication of 'b' and 'v'

B. Multiplying three digit numbers by two digit numbers
For abc x uv

The middle parts are obtained by adding the crosswise multiplications for a and b with v and u respectively, then b and c with v and u respectively. The outer parts are vertical multiplication of a with u on the left, c with v on the right.
Multiply:
1) vertically                                              (a x u)
2) crosswise in both directions and add    (a x v) + (b x u)
3) crosswise in both directions and add    (b x v) + (c x u)
4) vertically                                              (c x v)

The answer has the form:  au | av + bu | bv + cu | cv

Let us take an example: 236 x 53
   2       3       6
           5       3
-------------------------
  10 | 6+15 | 9+30 | 18
= 10 |  21  |  39  | 18

Work right to left carry over
= 10 | 21 | (39+1) | 8
= 10 | 21 | 40 | 8
= 10 | (21+4) | 0 | 8
= 10 | 25 | 0 | 8
= (10+2) | 5 | 0 | 8
= 12 | 5 | 0 | 8
236 x 53 = 12508

C. Multiplying four digit by two digit numbers
For abcd x uv

Multiply:
1) vertically                                              (a x u)
2) crosswise in both directions and add    (a x v) + (b x u)
3) crosswise in both directions and add    (b x v) + (c x u)
4) crosswise in both directions and add    (c x v) + (d x u)
5) vertically                                              (d x v)

The answer has the form:  au | av + bu | bv + cu | cv + du | dv

Example: 1348 x 74
  1      3      4      8  
                7      4
-------------------------------
 7 | 4+21 | 12+28 | 16+56 | 32
= 7 | 25 | 40 | 72 | 32
= 7 | 25 | 40 | (72+3) | 2
= 7 | 25 | 40 | 75 | 2
= 7 | 25 | (40+7) | 5 | 2
= 7 | 25 | 47 | 5 | 2
= 7 | (25+4) | 7 | 5 | 2
= 7 | 29 | 7 | 5 | 2
= (7+2) | 9 | 7 | 5 | 2
= 9 | 9 | 7 | 5 | 2
 1348 x 74 = 99752  

D. Multiplying five digit by two digit numbers
For abcde x uv

Multiply:
1) vertically                                              (a x u)
2) crosswise in both directions and add    (a x v) + (b x u)
3) crosswise in both directions and add    (b x v) + (c x u)
4) crosswise in both directions and add    (c x v) + (d x u)
5) crosswise in both directions and add    (d x v) + (e x u)
6) vertically                                              (e x v)

The answer has the form:  au | av + bu | bv + cu | cv + du | dv + eu | ev

Example: 12345 x 58
  1      2      3      4      5      
                       5      8
---------------------------------------
 5 | 8+10 | 16+15 | 24+20 | 32+25 | 40
= 5 | 18 | 31 | 44 | 57 | 40
= 5 | 18 | 31 | 44 | (57+4) | 0
= 5 | 18 | 31 | 44 | 61 | 0
= 5 | 18 | 31 | (44+6) | 1 | 0
= 5 | 18 | 31 | 50 | 1 | 0
= 5 | 18 | (31+5) | 0 | 1 | 0
= 5 | 18 | 36 | 0 | 1 | 0
= 5 |(18+3) | 6 | 0 | 1 | 0
= 5 | 21 | 6 | 0 | 1 | 0
= (5+2) | 1 | 6 | 0 | 1 | 0
= 7 | 1 | 6 | 0 | 1 | 0
 12345 x 58 = 716010

I hope it will help in quick multiplication. If there is any query, please post it here. In next article, we shall continue to discuss this technique for multiplying three digits by three digits numbers.


If you like the article, you may contribute by:

• Posting your comments which will add value to the article contents
• Posting the article link on Social Media using the Social Media Bookmark bar
• Connecting with 'VedantaTree' on Facebook (https://www.facebook.com/VedantaTree)

Vedic Math - Squaring numbers near base

In the previous article, we have discussed about the method of multiplication by using the base value. In this article, we shall learn the squaring of numbers by using base value. Squaring numbers near base is much easier as there is no possibility of different cases that we discussed earlier for multiplication, like
1. One number is above the base and the other number is below it
2. Numbers near different bases like multiplier is near to different base and multiplicand is near to different base.

So it is comparatively simpler. Here, we can use the sub sutra “whatever the extent of its deficiency, lessen it still further to that extent; and also set up the square of that deficiency”.

In this, first corollary is “All from 9 and the last from 10”. This method will work for any type of squaring. There is another method by taking the sutra "Vertically and Crosswise" but that we will discuss later.

Suppose we have to find the square of 8. The following will be the steps for it:
1. We shall take the nearest power of 10 (10 itself in this case) as our base.
2. 8 is '2' lesser than 10, so we shall decrease 2 from 8 (i.e. 8 - 2 = 6). This will become the left side of answer.
3. And, for right part of answer, we write down the square of that deficiency i.e. 2 x 2 = 4
4. Thus 8 x 8 = 64

In exactly the same manner, we say
7² = (7-3)  |  3²
     =  4  |  9
     =  49

9² = (9-1)  |  1²
     =  8  |  1
     =  81

6² = (6-4)  |  4²
     =  2     |     6                (Here, since right side is 2 digit number, so '1' will be carried to its left)
                   1
     =  3     |   6        
     =  36

Now, if numbers are above base value, approach will be almost same.  The only difference will be that instead of reducing the number from its deficiency, we increase the number by the surplus. For example,square of 13:

Here working base is 10.
13² = (13+3)  |  3²
       =  16  |  9
       =  169

See few more examples:
14² = (14+4)   |   4²
       =  18  |  16            (Carry over 1)
       =  19  |  6
       =  196

15² = (15+5)   |   5²
       =  20  |  25            (Carry over 2)
       =  22  |  5
       = 225

19² = (19+9)   |   9²
       =  28  |  81            (Carry over 8)
       =  36  |  1
       =  361

And then, extending the same rule to numbers of two or more digits, we proceed further as:

98² = (98-2)  |  2²
       = 96  |  04
       = 9604

93² = (93-7)  |  7²
       = 86  |  49
       = 8649

106² = (106+6)  |  6²
         =  112  |  36
         =  11236

986² = (986-14)  | 14²
         =  972 | 196
         =  972196
 
9996² = (9996-4)  |  4²
           =  9992 |  0016
           =  99920016  

Note: Number of digits in right side part of the answer should always be equal to the zeros in the base value. Extra should be carried forward to left side answer. If number of digits in right side answer are less than the zeros, then it should be prefixed by zeros.
 
The Algebraic Expressions are as follows:

       (a + b)² = a² + 2ab + b² 

Thus,
97² = (100-3)²
       = 10000 - 600 + 9
       = 9409

107² = (100+7)²
         = 10000 + 1400 + 49
         = 11449
 
Another case arise here that if numbers are not near the base value (i.e. where base value is not power of 10). In that case we follow the same method as we discussed in our previous article. For example: 29² . Here working base is 30. So,
29²
 29    -1
 29    -1
-----------
 28  |  1
= 28 x 30  |  1       (multiply the left part of answer with the base)
= 840 |  1
= 840 + 1
= 841

Another example to understand it more: 786² . Here working base is 800.
786²
 786    -14
 786    -14
-------------
 772  |  196
= 772 x 800  |  196
= 617600 | 196
= 617600 + 196
= 617796

So this is all about squaring the numbers by using the base values. Isn't that quite simple and interesting approach.. In next article, we shall discuss about Vertical and Crosswise multiplication.

If you like the article, you may contribute by:

• Posting your comments which will add value to the article contents
• Posting the article link on Social Media using the Social Media Bookmark bar
• Connecting with 'VedantaTree' on Facebook (https://www.facebook.com/VedantaTree)

Vedic Math - Base Multiplication Part-2

In the previous article, we learnt multiplication by taking base. We discussed following three cases:
A. Numbers are below the base number
B. Numbers are above the base number
C. One number is above the base and the other number is below it

And now, we shall discuss rest of the two cases here:
D. Numbers are not near the base number, but are near a multiple of the base number, like 20, 30, 50 , 250 , 600 etc.
E. Numbers near different bases like multiplier is near to different base and multiplicand is near to different base.

Before going further, let us take few examples of larger numbers with the same method, which we have discussed in previous article.

Example: 6848 x 9997

 6848    -3152
 9997    -0003
----------------
 6845  |  9456     (Refer to previous article for details of approach)
----------------

Example: 87654 x 99995

Let us discuss the fourth case:
D. Numbers are not near the base number, but are near a multiple of the base number, like 20, 30, 50 , 250 , 600 etc.

As you know that this method is applicable in all the cases, but works best when numbers are close to the base. Here, we shall apply the same sutras  “All from 9 and the last from 10” and "Vertically and Crosswise"  discussed earlier and also the sub sutra i.e. "Proportionately".

Take example as 207 x 213 . Here the numbers are not near to any of the bases that we used before: 10, 100, 1000 etc. But these are close to '200'. So, when neither the multiplicand nor the multiplier is near to the convenient power of 10 then we can take a convenient multiple or sub-multiple of a suitable base (as our 'Working Base'). And then perform the necessary operation by multiply or divide the result proportionately. Like in this example, we take 100 as a 'theoretical base' and take multiple of 100 i.e. 200 (100 x 2) as our 'working base'.

207 x 213
  207    +007
  213    +013
  ------------
= 220  |  091
  ------------
= (220 x 200) | 91
= 44000 + 91
= 44091

As they are close to 200, therefore deviations are 7 and 13 as shown above. From the usual procedure (refer to previous article), we get, 220 | 91. Now since our base is 200, we multiply the left-hand part of the answer by 200 and add it to the right-hand part. That is, (220 x200) + 91 {(Left side x base) + right side}. The final answer is '44091'.

Let us take one more example: 406 x 417
Here Working base is 400 ,which is (100 x 4)

   406    +06
   417    +17
   ------------
 = 423  |  102  
   ------------
 = 423 x 400  |  102
 = 169200  |  102
 = 169200 + 102
 = 169302

Another example is, 46 x 43. We can solve it in two ways:
First, we take 10 as a theoretical base and take multiple of 10 i.e. 50 (10 x 5) as our working base.
Second, we take 100 as a theoretical base and take sub-multiple of 100 i.e. 50 (100/2) as our working base.

 46    -4
 43    -7
-----------
 39  |  28
-----------
From our usual procedure, we get 39 | 28. Now,
First way (10 x 5 = 50):
1. Multiply the left-hand part of the answer by 50 (39 x 50)and get 1950 as the first part.
2. Now add 1950 to 28 and get 1978.
3. Final answer is '1978'

Second way (100/2 = 50):
1. Divide the left-hand part of the answer by 2 and get 19.5
Note:-Here 39 being odd, its division by 2 gives us a fractional quotient or decimal number.So, number after decimal(i.e. 5) of the left hand side is carried over to the right hand (as 50).
2. Left-hand part is now '19' and right-hand part is 78(i.e. 50 + 28)
3. Final answer is: 1978

In the above discussed two examples, we can also apply the second method. Like in 207 x 213 , we can also take working base: 1000/4 = 250 or 1000/5 = 200. And in 406 x 417 , we can also take working base: 1000/2 = 500. We have to choose the best convenient multiple or sub-multiple.

Following an example in which you solve it in many ways:
 62 x 48

(1) Working Base 10 x 4 = 40          
        62    +22                                          
        48    + 8                                      
       -----------
        70  |  176                                       
       x40                                                    
       -----------                                          
       2800 |  176                                      
       -----------                                        
       = 2800 + 176                                                                                            
       = 2976          
                                                       
(2) Working Base 10 x 6 = 60        
        62    + 2                                         
        48    -12                                          
       ----------                                      
        50  | -24                                   
       x60                          
       -----------                                    
       3000 | -24                                        
       -----------                                          
       = 3000 - 24                                        
       = 2976                                           

(3) Working Base 10 x 5 =50
        62    +12                                      
        48    - 2                                          
       ----------                                        
        60  | -24                                 
       x50                            
       -----------                                            
       3000 | -24                                          
       -----------                                          
       = 3000 - 24                                          
       = 2976                                               

(4) Working Base 100/2 = 50
        62    +12                                      
        48    - 2                                          
       ----------                                        
        60  | -24                                 
        /2                            
       -----------                                            
        30  | -24                                          
       -----------                                          
       = (30 x 100) - 24                                          
       = 2976

Example: 43 x 47
In this, the base is 100/2 = 50 , so divide the left side by 2 to get the answer.
    43   -7                             (as above we subtract 50 from our numbers)
    47   -3
   ----------
   40  |  21                          

   /2                                     (calculate the left side, then divide the answer by 2)
  -----------
   20  |  21
  -----------
  =(20 x 100) + 21
  =2021
This gives: 43 x 47= 2021

E. Numbers near different bases i.e. 'multiplier' is near to one base and multiplicand is near to other base.
Many of times we need to multiply numbers that are not near to same base but are near to different bases.
In the example given below, you find that one number is close to 1000 and the other is close to 100.

Example: 996 × 97
= 996 × (97 x 10) / 10            (can be rewritten like this)
= 966 x 970 / 10                     (which can futher be written like this)

Let us first solve 966 x 970
996   –004
970   –030
------------
966 |  120
------------
= 966 x 1000 + 120              (multiply left side result by base)
= 966000 + 120
= 966120

So the answer for 966 x 970 is 966120

Now we shall solve the complete equation i.e. will divide it by 10,
  = 966120 / 10
  = 96612

So 996 x 97 = 96612

Example: 10005 x 1002
Here the numbers are close to different bases: 10000 and 1000

So equation can be written as
= 10005 x (1002 x 10) / 10

Now let us solve 10005 X 10020 first

10005     + 005
10020     + 020
-----------------
10025   |   0100
= 10025 x 10000 + 100         (multiply left side result by base)
= 100250000+ 100
= 100250100

So 10005 X 10020 = 100250100
Now let us solve the original equation i.e. will divide the answer by 10
= 100250100/10
= 10025010

So 10005 x 1002 = 10025010

Example: 212 x 104
Rewrite as : 2 x (106 x 104)
            = 2 x 11024
            = 22048

Example: 192 × 44.
Here you can halve 192 and double 44.
= 192 x 44
= (192 / 2) x (44 x 2)              (divide by 2 and multiple by 2)
= 96 x 88

Now solve this equation by procedure defined above
= 96 × 88
= 8448.

If you like the article, you may contribute by:

• Posting your comments which will add value to the article contents
• By Posting the article link on Social Media using the Social Media Bookmark bar
• By Connecting with 'VedantaTree' on Facebook (https://www.facebook.com/VedantaTree)    

Vedic Math - Base Multiplication

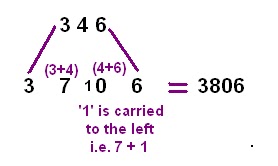
Today, we are going to learn the GENERAL formula of multiplication. This is simple and easy technique and good part is that it is applied to almost all the cases. This method works better when numbers are near their base value. After going through the below discussed method, you will see that multiplication tables are not required for calculation above 5 x 5. You will be able to do all types of multiplication involving bigger multiplicands and multipliers quickly and easily; like for '789789 × 999997'. All the sutras (formulae) of Vedic Math are short and simple; and with the practice of the techniques, most of the calculations become a playful experience for you.

Following is the sutra that we will follow today:

The formulae (sutras) are : “All from 9 and the last from 10” and "Vertically and Crosswise"
The algebraical expression is :(x+a) (x+b) = x (x+a+b) + ab.

From the title of the article, you can understand that today we shall do the multiplication by taking the base of numbers. So, first we need to be familiar what is 'base'. The term ‘base’ in Vedic Math has a broader meaning than you may be used to. We work in a base 10 number system, but within Vedic Math the ‘base’ is the number you will use as a basis for calculation. The numbers taken can be either less or more than the base considered. The difference between the number and the base is termed as deviation. Deviation may be positive or negative.

Now observe the following table.

Number      Base         Number – Base       Deviation
   13             10                  13 - 10                      3

    7              10                     7 - 10                    -3

   89             100                  89 - 100                -11

 1110           1000             1110 - 1000              110

99998          100000       99998 - 100000            -2

So, the deviation obtained are from "All from 9 and the last from 10" sutra (formula).

Following are the cases which we shall discuss here:
A. Numbers are below the base number
B. Numbers are above the base number
C. One number is above the base and the other number is below it
D. Numbers are not near the base number, but are near a multiple of the base number, like 20, 30, 50 , 250 , 600 etc
E. Numbers near different bases like multiplier is near to different base and multiplicand is near to different base

Let us discuss these cases one by one.

A. Numbers are below the base number

Working with Base 10
Let us take an easy and simple example to start this technique. Suppose we have to multiply 6 by 8.
Now the base is 10. Since it is near to both the numbers.
Place the two numbers 6 and 8 above and below on the lefthand side (as shown below). Subtract the base value (i.e. 10 in this case) from both of the numbers and write down the remainders (i.e. 4 and 2) on the right-hand side with their deviation sign (-).

6 x 8   

Left side (4 ways to calculate left side)
a) 6 + (- 2)= 4                   (add top left to bottom right)
b) 8 + (- 4)= 4                   (add bottom left to top right)
c) 6 + 8 - 10= 4                 (add numbers in the left column and subtract from base)
d) 10 + (-4)+(-2)= 4          (add numbers in the right column and the base)

Right side
(-4) x (-2) = 4                   (multiply numbers of right column)

Final answer: 6 x 8= 48

Some more examples of the same rule:

 9 x 9            9 x 8              8 x 7            8 x 8               7 x 9
 9    -1          9    -1             8    -2           8    -2             7    -3
 9    -1          8    -2             7    -3           8    -2             9    -1
---------          ----------        ----------         ----------         -----------
 8     1            7     2            5     6            6     4             6     3
---------          ----------        ----------         -----------        -----------

This comes under the "Vertically and Crosswise" Sutra.

Sometimes there can be a carry figure, so let’s have a look on the next example.
 6 x 6
6     -4
6     -4
---------
2   |   6
       1
---------
But here, as '16' is a two digit number, so you need to carry the 1 over to the left side i.e. '2'. Therefore, left hand side now becomes (2 + 1 = 3).
And Final answer : 6 x 6 = 36

Following are some of the examples:

 8 x 5            7 x 6          6 x 5            7 x 5
 8    -2          7    -3         6    -4           7    -3
 5    -5          6    -4         5    -5           5    -5
--------          ----------       ---------       -----------
3  |    0           3  |    2        1  |    0         2  |    5
      1                   1                 2                  1
--------           ----------      ----------      ------------
 = 40              = 42            = 30            = 35

Working base 100
Example: 96 x 98

96    -04
98    -02
---------
94  |  08   =   9408
---------

Working base 1000
Example: 998 x 988

998    -002
988    -012
------------
986  |  024    =   986024
------------

B. Numbers are above the base number. Process will be same as described above.

Working with Base 10
Suppose we have to multiply 13 by 14.
Now the base is 10. Place the two numbers 13 and 14 above and below on the lefthand side (as shown below). Subtract  base (10) from each of the numbers and write down the remainders (3 and 4) on the right-hand side with their deviation sign (+).
 13 x 14
 13      +3                          (as before,subtract 10 from both numbers)
 14      +4
-----------
 17  |    2
          1           = 182
-----------

Left side (4 ways to calculate left side)

a) 13 + (+ 4)= 17                       (add top left to bottom right)
b) 14 + (+ 3)= 17                       (add bottom left to top right)

c) 13 + 14 - 10= 17                   (add numbers in the left column and subtract from base)
d) 10 + (+ 3) + (+ 4)= 17           (add numbers in the right column and the base)

Right side
(+3) x (+4) = 12                   (multiply numbers of right column)

Since 12 is  2-digit number, so carry the 1 over to the 7. Therefore, left hand side is now
(17 + 1 = 18). And Final answer : 13 x 14 = 182

Some more examples of the same rule :-

 12 x 11      16 x 12      13 x 15      14 x 12
 12   +2       16   +6       13   +3       14   +4
 11   +1       12   +2       15   +5       12   +2
---------        ---------       ---------        ----------
 13  |   2      18  |   2      18  |   5        16  |  8
                           1               1
---------        ---------        ---------        ----------
 =132          =192           =195          =168

Working base 100
Example: 102 x 107

102     02
107     07
-----------
109  |  14   = 10914
-----------

Working base 1000
Example: 1005 x 1003

1005     005
1003     003
-------------
1008  |  015   =  1008015
-------------

C. One number is above the base and the other number is below it
In this, one deviation is positive and the other is negative. So the product of deviations becomes negative. So the right hand side of the answer obtained will therefore be subtracted i.e. right side answer get subtracted from (left side answer x base )

Working with Base 10
Suppose we have to multiply 13 by 4
The nearest base is 10.
 13 x 4
 13    +3                   (as before, subtract 10 from both numbers)
  4     -6
----------
  7  |  -18    = 7 x 10 - 18  =  70 - 18  =  52
----------

Left side(4 ways to calculate left side)

a) 13 - 6= 7                        (add top left to bottom right)
b) 4 + 3= 7                         (add bottom left to top right)

c) 13 + 4 - 10= 7                (add numbers in left column, subtract 100)
d) 10 + (+ 3) + (- 6)= 7      (add numbers in the right column and the base)
Right side
(+3) x (-6) = -18                 (multiply numbers of right column)
                         __
So, 13 x 4 = 7 | 18
           = (7 x 10) - 18          (right side answer get subtracted from (left side answer x base ))
           = 70 - 18
           = 52  
Final answer : 13 x 4 = 52

Following are some of the examples:-

 12 x 8            14 x 6             13 x 3          15 x 7
 12    +2         14    +4           13   +3        15    +5
  8     -2           6     -4             3    -7           7    -3
-----------         ----------         ---------         ----------
 10  | -4           10  |  -16         6  | -21       12  |  -15
-----------         ----------         ---------         ----------
 =100-4           =100-16         =60-21        =120-15
 =96                 =84                =39              =105

Working base 100
Example: 102 x 97

102     02
 97    -03
-----------
 99  | -06
----------
  = 9900-6
  = 9894

Working base 1000
Example: 1005 x 993

1005      005
 993     -007
--------------
 998  |  -035
--------------
 = 998000-35
 = 997965

We shall discuss about rest of the two cases in next article. Stay tuned!!

Next Article will cover:
D. Numbers are not near the base number, but are near a multiple of the base number, like 20, 30, 50 , 250 , 600 etc.
E. Numbers near different bases like multiplier is near to different base and multiplicand is near to different base.

If you like, you may contribute by

·        Posting your comments which can add to the article contents
·        By Posting the article link on Social Media using the Social Media Button bar
·        By Connecting with 'VedantaTree' on Facebook (https://www.facebook.com/

VedantaTree)

Thank you!

Vedic Math - Mathematical magic trick

Let us take a break from calculations and enjoy a small magical mathematics trick.

1. Think a number (any number). To keep it easy, think any number having 1 or 2 digit.
2. Now double this number i.e. multiple by 2.
3. Add 12 to the result
4. Divide the total by 2.
5. Subtract the original number from above result.
6. And you will always get '6' as final result.

Try this one with different numbers, and you will see that the sequence always produces the '6' as result ,no matter which number was originally selected.

For example, if the original number is 15.
1. 2 x 15 = 30
2. 30 + 12 = 42
3. 42 / 2 = 21
4. 21 - 15 = 6

You must be curious that how this magic trick is working. Following is the concept for this magic trick:

Let us take a number be x and the steps performed by us are:
1. 2x
2. 2x + 12
3.(2x + 12) / 2 = x + 6
4. x + 6 - x = 6

So, in last step, we see that whatever number we choose (as x) will finally result in '6' with above calculation. After knowing the formula, now you can change the answer by changing the formula. For example, if you want to change the answer to '4', then you add twice of that '4' i.e. '8' in the second step.

Enjoy this trick!!

Vedic Math - Multiplication of numbers whose last digits add to 10 and first digits are same and vice-versa.

We had discussed this method in our previous articles for 2-digit numbers and today we shall explain the same method for 3-digit numbers.

A. Numbers whose last digits add to 10 and the remaining first digits are the same
Case 1: When sum of last two digits number is 100 
Example: 392 x 308
Here we can see that right digits sum is 100 i.e.(92 + 8) and left side digits are same. Here we can now apply the same method, which we discussed earlier for 2-digit number. But this time we must expect to have four figures on the right-hand side.

• First, multiply the right side numbers(92 x 08) and the result is 0736.
• Second, multiply 3 by the number that follows it, i.e.4, so the result of (3 x 4) is 12.
• And now the final output is 120736.

Example: 795 x 705
Here 95 + 05 = 100 and left side digits are same i.e. '7'. Hence it qualifies for this case.
In calculation, we shall multiple the last two digits and the left digit i.e. '7; with its next number '8'. So the calculation is:
795 x 705 = 7 x 8 | 95 x 05
                 = 56 | 0475
                 = 560475

Example: 866 X 834
Here 66 + 34 = 100 and left side digit is 8 and its next number is 9. So the calculation is:
848 x 852 = 8 x 9 | 66 x 34            (Note: For 66 x 34, we shall discuss in our upcoming articles)
                 = 72 | 2244
                 = 722244
         
         
Case 2: When sum of whose last digits is 10  and the remaining first digits are the same   
Example: 241 x 249
Here we can see that right digits sum is 10 i.e.(9 + 1) and left side digits are same i.e. 24. So we can now apply the same method as described above.
241 x 249 = 24 x 25 | 1 x 9
                 = 0600 | 09
                 = 60009

444 x 446 = 44 x 45 | 4 x 6
                 = 1980 | 24
                 = 198025
         
147 x 143 = 14 x 15 | 7 x 3
                 = 0210 | 21
                 = 21021

Special cases:
Case 1: Where numbers are not qualified for above case in general, but can be qualified after converting their form. Example is given below.

For example: 93 x 39
93 × 39 doesn't seems to comes under this method. But if we convert 93 to (3 × 31), then 31 × 39 comes under this method. So the calculation is
93 x 39 = 3 x 31 x 39
             = 3 x (31 x 39)
31 × 39 = 1209            (by same method discussed above i.e. 31 x 39 = (3 x 4) | (1 x 9) = 12 | 09 = 1209)
93 × 39 = 3 x 1209
             = 3627
         
The point to notice in the above example is that '39' needs '31' to qualify for method, and then we found that 93 is '3 × 31'.


Case 2: If the left hand digits are the same, but last digit's sum is not 10. We can still apply the same method that we discussed just above. For example: 35 x 37

In 35 x 37, both left hand numbers are 3, but 5 + 7 = 12 which is greater than 10. We can solve this in two ways.

First, we modify the numbers in such a way that we can apply the method used for "squaring numbers ending in 5":
35 x 37 = 35 x (35 + 2)
        = (35 x 35) + (35 x 2)   
        = 1225 + 70           (Take 35 x 35 = 3 x 4 | 5 x 5 = 12 | 25 = 1225)
        = 1295

Second approach is, we modify the numbers in such a way that we can apply the method discussed above. So we split 35 as 33 + 2. And observe that (33 x 37) comes under the above discussed method.
So, we rewrite it as:
35 x 37 = (33 + 2) x 37
        = (33 x 37) + (2 x 37)
        = 1221 + 74           (Take 33 x 37 = (3 x 4) | (3 x 7) = 12 | 21 = 1221)
        = 1295

One more example:
114 x 117 = 114 x (116 + 1)
          = (114 x 116) + (114 x 1)
          = 13224 + 114       (Take 114 x 116 = (11 x 12) | (4 x 6) = 132 | 24 = 13224)         
          = 13338
OR
114 x 117 = (111 + 3) x 117   (Rest of the procedure is same)

Now, take one more example where first digit remains same but addition of last digits is less than 10.
68 x 61 = 68 x (62 - 1)
        = (68 x 62) - (68 x 1)  (Rest of the procedure is same)
OR
68 x 61 = (69 - 1) x 61
        = (69 x 61) - (61 x 1)    (Rest of the procedure is same)   

B.Numbers whose last digits are same and first digits add to 10

Now let us solve some case where last figures are the same and the first figures add up to 10. This comes under the Vedic formula "The First by the First and the Last by the Last". For example: 47 x 67
Here we can see that left hand digits sum is 10 i.e.(4 + 6) and right hand digits are same i.e. 7 . So we can now apply the following method.

• Multiply the first digit of each number together i.e.(4 x 6 = 24). Add the last figure (7) into it (24 + 7 = 31) which is the first part of the answer.
• Multiplying the last figures together(i.e.7 × 7 = 49) which is the last part of the answer.
• The final answer is 3149.

Let us take some more examples

34 x 74 = (3 x 7) + 4 | 4 x 4
        = 21 + 4 | 16
        = 2516

98 x 18 = (9 x 1) + 8 | 8 x 8
        = 9 + 8 | 64
        = 1764
       
23 x 83 = (2 x 8) + 3 | 3 x 3
        = 16 + 3 | 09
        = 1909   

Note: You can do "Squaring of numbers between 50 and 60" with the same method. You might be thinking that how this could be. But see, left hand digits sum is 10 i.e.(5 + 5) and right hand digits are same. So we can now apply the same method. We had already discussed it in "squaring numbers near 50", both are almost same but different presentation. See the following example:

58²= 58 x 58
     = (5 x 5) + 8 | 8 x 8
     = 25 + 8 | 64
     = 3364
   
53²= 53 x 53
     = (5 x 5) + 3 | 3 x 3
     = 25 + 3 | 09
     = 2809
   

How do you like these Vedic Maths technique, please let us know.

Vedic Math - Multiplication of numbers with a series of 1's

In the previous article, we learnt the technique of "how to multiply numbers with a series of 9’s". In this article, we shall learn the technique of "how to multiply numbers with a series of 1’s". So, we shall multiply the numbers with 1, 11, 111,..... etc.

I. Let us start with the vedic multiplication by 11

In this technique, we use "vertically and crosswise" vedic sutra. Take example of ab x uv, and apply the sutra as follows:

       a         b
       u         v
   ---------------------
   a x u | av + ub | b x v
   ---------------------

(Here '|'  is used just as separator)

Here we are splitting the answer in three parts as following:

• vertically                         =(b x v)
• crosswise multiplication and add   =(a x v) + (b x u)
• vertically                         =(a x u)

During multplication with 11, u=1 and v=1, means:

           a               b
           1               1
         --------------------
           a  |  a + b  |  b
         --------------------


Example:  Multiply 53 by 11

Here one point to consider is that we should write the answer from right to left. Because, in case, sum of the digits of multiplicand comes in 2 digits, we need to carry the ten's place digit to next (left side) calculation. You will notice it in next examples.

Example:  Multiply 68 by 11

Step 1 : Last part of the answer is same as the last part of the multiplicand i.e. 8 (8 x 1). > 8
Step 2 : For middle part, sum the digits of multiplicand i.e. 6 + 8 = 14. We will not write '14' as the middle  part. We write down '4' and digit '1' is carried over. > 4
Step 3 : First part is now, first digit of multiplicand i.e. 6. But we have one digit as carry from step 2, so we shall add this to first part. Now first part will become 6 + 1 = 7. > 7

Finally, answer is 748.

Some examples are given below:
54 x 11= 5 | 9 | 4 = 594
35 x 11= 3 | 8 | 5 = 385
81 x 11= 8 | 9 | 1 = 891
96 x 11= 9 | 15 | 6 = 10 | 5 | 6 = 1023 ( here '1' carry over)
88 x 11= 8 | 16 | 8 = 9 | 6 | 8 = 968   (again '1' carry over)


This technique is also applicable to numbers having more than 2 digits. You just need to take first and last digits of multiplicand as it is (as done in previous examples), and continue adding the adjacent two numbers for middle parts (more than one parts now).

Example: Multiply 346 by 11

Following examples will help to understand more.

267 x 11   = 2 | 2+6 | 6+7 | 7          
                =  2 | 8 | 13 | 7       
                = 2 | 9 | 3 | 7      
                = 2937                   
        
2678 x 11  = 2 | 2+6 | 6+7 | 7+8 | 8   
                 =  2 | 8 | 13 | 15 | 8  
                 = 2 | 9 | 4 | 5 | 8  
                 = 29458    

26789 x 11 = 2 | 2+6 | 6+7 | 7+8 | 8+9 | 9
                  =  2 | 8 | 13 | 15 | 17 | 9
                  = 2 | 9 | 4 | 6 | 7 | 9
                  = 294679 


II. Now, let us learn to multiply any number with 111.

In this, since multiplier is 3-digit number, so for middle part, we shall start by adding first two digits and then keep on adding next three ( and next three and so on) and then will end by adding the last two digits. First and last part will be same as described above. You will understand this with following examples.

Examples:

365 x 111    = 3 | 3+6 | 3+6+5 | 6+5 | 5          
                   = 3 | 9 | 14 | 11 | 5              
                   = 40515

3645 x 111   = 3 | 3+6 | 3+6+4 | 6+4+5 | 4+5 | 5        
                    = 3 | 9 | 13 | 15 | 9 | 5             
                    = 404595 

567894 x 111  = 5 | 5+6 | 5+6+7 | 6+7+8 | 7+8+9 | 8+9+4 | 9+4 | 4
                       = 5 | 11 | 18 | 21 | 24 | 21 | 13 | 4                    
                       =   63036234

57 x 111     = 057 x 111    
                  = 0 | 0+5 | 0+5+7 | 5+7 | 7      
                  = 0 | 5 | 12 | 12 | 7   
                  = 06327 = 6327  


III. Similarly, we can multiple any number by 1111.

In this, since multiplier is 4-digit number, so for middle part, we shall start by adding first two digits, then first three digits and then keep on adding next four ( and next four and so on) and then will end by adding the last three digits, and then last two digits. First and last part will be same as described above. You will understand this with following examples.

Examples:

5678 x 1111   = 5 | 5+6 | 5+6+7 | 5+6+7+8 | 6+7+8 | 7+8 | 8          
                      = 5 | 11 | 18 | 26 | 21 | 15 | 8          
                      = 6308258

126453 x 1111 = 1 | 1+2 | 1+2+6 | 1+2+6+4 | 2+6+4+5 | 6+4+5+3 | 4+5+3 | 5+3 | 3
                        = 1 | 3 | 9 | 13 | 17 | 18 | 12 | 8 | 3   
                        = 140489283

43 x 1111         = 0043 x 1111     
                        = 0 | 0+0 | 0+0+4 | 0+0+4+3 | 0+4+3 | 4+3 | 3                              
                        = 0 | 0 | 4 | 7 | 7 | 7 | 3                       
                        = 47773

Using the same method, we can multiply any number by a series of 1’s. If you want to multiply a number by 11111 (irrespective of how big is the multiplicand), the only difference will be that we will add maximum five numbers at a time for middle part of answer(because there are five ones in 11111).

And remember the basic rule that we use in normal addition — carry over the digit to its left when you have a two-digit answer.

Vedic Math - Multiplication of numbers with a series of 9’s

Another special case of multiplication is, multiplication with numbers like 9, or 99, or 999, or 9999.....so on. It feels like if multiplier is a big number, the calculation will be tough. But, with the help of vedic math formulae, the multiplication is much easier for all '9' digits multiplier. By using the method given below, we can multiply any number with 99,999,9999, etc. very quickly.

Please note that the methods or the vedic formulae, that we use in this calculation, are "By one less than the one before"  and "All from 9 and the last from 10".

There are three cases for the multiplication of numbers with a series of 9's.

• Case 1: Multiplying a number with a multiplier having equal number of 9’s digits                                              (like 587 x 999)
• Case 2: Multiplying a number with a multiplier having more number of 9’s digits                                             (like 4678 x 999999)
• Case 3: Multiplying a number with a multiplier having lesser number of 9’s digits                                             (like 1628 x 99)

The method to solve 'Case 1' and 'Case 2' is the same, but for 'Case 3', the method is different. Let us start with 'Case 1'.

Case 1: Multiplying a number with a multiplier having equal number of 9’s digits

Multiply 587 by 999

           587
       x  999
       ------------
        586 413
       
Solution is,

•  Let us first do the calculation by conventional method to understand the solution. Result will be 586413.
• Split the answer in two parts i.e. '586' and '413'.
• Let's see the first part of the result, i.e. 586. It is reduced by 1 from the number being multiplied i.e. 587 - 1 = 586. {Vedic sutra "By one less than the one before"}
• Now see the last part, i.e. 413. Subtract the multiplicand i.e. 587 from 1000 (multiplier + 1). Vedic Sutra applied here is "All from 9 and the last from 10", and hence we substract 587 from 1000. So the outcome will be (9 -5 = 4, 9 - 8 = 1, 10 - 7 = 3) , and result is 413. Refer to image below for more clarity:

Case 2: Multiplying a number with a multiplier having more number of 9’s digits
Multiply 4678 by 999999

           4678
     x   999999
   ----------------
    4677 995322   

Here, 4678 is 4-digit number and 999999 is 6-digit number. So, we can rewrite 4678 as 004678 to make 6-digit number. Now, it turns out to be same as case 1. So, same method is going to be applied.

The result has two parts:

• The first part of the result, i.e. 4677, which is reduced by 1 from the number being multiplied      (4678 - 1). {Vedic sutra "By one less than the one before"}
• For the last part of answer (995322), Subtract the multiplicand i.e. 004678 from 1000000   (1000000 - 004678). Here we are applying the vedic formula "All from 9 and the last from 10" on 004678. Calculation is like:

•  9 - 0  =9
•  9 - 0  =9
•  9 - 4  =5
•  9 - 6  =3
•  9 - 7  =2
• 10 - 8 =2

• So the result is 995322
• Now combine first and last part, and you get the final answer i.e. '4677995322'

Case 3: Multiplying a number with a multiplier having lesser number of 9’s digits

Multiply 1628 by 99

For this case, method is changed. In this, we rewrite 1628 x 99 as 1628 x (100 - 1). So,

                     1628(100 - 1)
                   = 162800 - 1628
                   = 161172

Here, calculation might get slow during substraction. But once you learn the vedic subtraction, it will become fast. In coming sessions, we shall discuss it.

OR  there is another approach given below, by spliting the solution in three parts.

                1628 x 99 = 16 : 11 : 72

Now, see how we get this result using Vedic Math:

                        16     : 28    : 100
                                 : 17    :   28
                      -----------------------  
                        16     : 11     :  72

                                                                                          
Steps to follow are given below:

• Split the multiplicand in such a way that the right hand side number contains the digits equal to the number of digits in multiplier. Like here, multiplier is 99 (having 2 digits). So after splitting the multiplicand, the right hand side number will be 28. Now, there are two parts of multiplicand after split i.e. 16 and 28.
• Create three different virtual columns, and place two parts of splited number in first and second column.
• In third column, put (multiplier + 1) i.e. 100 in this case
• Now add '1' to first part of multiplicand, and place it in middle column of second row. Number of digits should be equal to number existed in first row in same column. If it is not, shift the extra digits in first column of second row.
• Place second part of multiplicand (28, from first row) in third column.
• Now subtract numbers in second row from first row numbers, in their respective columns. In case of middle column, if first row number is lesser than second row number, we can borrow '1' from first column value.
• If we follow this, the answer for each column will be
• Third Column: 100 - 28 = 72
• Second Column: 28 -17 = 11
• First Column: 16 - 0 = 16
• So the answer is, '16 11 72'

Example where number in middle column of first row is lesser than second row value (63 x 9):
                6    : 3    :  _
                _    : 7    :  3
               -----------------
                5    : 6    : 7

Here, 3 is less than 7 and subtraction is not possible. Hence we borrow '1' from first column value i.e. borrow 1 from 6 and 3 becomes 13 and left part is now 5.

One more example to make it more clear: 17119 x 99

                       171   : 19   : _ _
                           1   : 72   :  19
                    ----------------------   
                       169   : 47   : 81


Here, don't get confuse by seeing '1' in the first column of second row. It is just taken from '172' (which is one more than '171'). As per the method, middle column should have number having digits equal to multiplier. So we shift '1' to first column. Rest all is same.

Hope you understandand this method. If you have any question, please post in comments. In the next session, we shall discuss about multiplication of numbers with a series of 1's.