Vedic Math - Divsion by 9

Let us learn, how to do 'Division' operation using 'Vedic Math'. Conventionally, we do it like following:

Divisor ) Dividend ( Quotient
                ---------
                ---------
             _________
             Remainder

However, in the Vedic process, the format is
Divisor ) Dividend
                --------
           __________________
           Quotient | Remainder

Let us first start with one of the special case of division i.e. Division By 9, a very interesting and simple technique.

When dividing by 9, the remainder is always the digit sum of the original number.

For 2-digit number divided by 9 
To divide ab by 9 : Rewrite ab as a | b . The quotient is a, and the remainder is simply a + b.

    a  |  b
        |  a
    ---------
    a  | a + b

Examples: 

12 divided by 9
Here quotient = 1 and remainder = 1+2 = 3

23 divided by 9
Here quotient = 2 and remainder = 2+3 = 5

70 divided by 9
Here quotient = 7 and remainder = 7+0 = 7

Now, let us discuss the cases when remainder is greater than 9 :-

Vedic Math - Cube Roots of more than 6-Digit Number - Part III

In this article, we are going to learn an interesting Mathematical technique to find, if the given number is a perfect cube or not. It is very important step while computing cube roots. Infact, before applying any method to find the cube root, we have to check whether it is perfect cube or not and then accordingly we choose the technique. For example, following scenario tells us the importance of finding perfect cube step while computing the cube root.

Example : 1728 has cube root 12 since two groups are 1 and 728. From 728, we derive last digit as                 2 from 1 (first group), we derive first digit as 1.
               So, cube root of 1728 is 12.
 But now, if number is 1278, which again has two groups: 1 and 278. It can derive the same last digit as 2 and first digit as 1 , which implies that cube root of 1278 is 12, which is not true because technique stands true for perfect cube root only.

There is a simple technique to check whether the number is perfect cube or not. For this, we add the digits of the number. See the below chart in which we add the digits of cubes from 1 to 10.

Above example shows that sum of digits of a perfect cube is either 1, 8 or 9. However, it is not true that all numbers which sum to 1,8 or 9, will be perfect cube.

For example,
Sum of digits of 1728 and 1278 are same i.e.(1+7+2+8) = (18) = 9 . But 1278 is not a perfect cube.

Hence if sum of digits of a number is not 1,8 or 9, we are very sure that the number is not a perfect cube. However, a number may not be perfect cube root even if sum of digits is 1,8 or 9. To scrutinize that, we need to apply factorisation. If number is small like 1278, factorisation is good method. See below:

For bigger numbers, factorisation could be time consuming technique. Hence, for large numbers, we shall apply general method of finding the cube of root.

Case 2 : Cube root for all the cubes, whether perfect cubes or not.    (Case 1 discussed in last two articles)
From last two articles, we conclude about the sequence of digits (a+b+c)³ as:
(1) The first place by a³
(2) The second place by 3a²b
(3) The third place by 3ab²+3a²c
(4) The fourth place by 6abc+b³
(5) The fifth place by 3ac²+3b²c
(6) The sixth place by 3bc²
(7) The seventh place by c³ ; and so on.

In 'General Technique', we find Dividends(D), Quotients(Q), and Remainders(R). Steps involved as:
(1) First determine D, Q and R
(2) From the second dividend, no deduction is to be made.
(3) From the third, subtract 3ab²
(4) From the fourth, deduct 6 abc+b³
(5) from the fifth, subtract 3ac²+3b²c
(6) from the sixth, deduct 3bc²
(7) from the seventh, subtract c³. ; and so on.

(a) Quotient(Q) is closest minimum exact cube to the first cube i.e. 'F' term used in last two articles.
(b) And, Reminder(R) is the difference between the first group and closest minimum exact cube.
(c) Dividend(D) is found by multiplying the 'Square of Quotient(Q)' by 3 (Q²*3)

Lets take an example to make it more clear.
Example 1 : 248858189

(1) First arrange the numbers in groups i.e. 248,858,189
Here, N = 3
First group(248) has closet minimum exact cube (216) which is 6³. So, First Quotient(Q) = 6
First Reminder(R) = 248-216 = 32
First Dividend(D) = 6²*3 = 108

(2) The second Gross Dividend is 328. We don't subtract anything at that point. We only divide it by 108 and write down 2 and 112 as Q and R.
[Important Note : Here we are taking quotient to be 2 instead of 3; because if we take it as 3, the reminder comes out 4 (328-108*3) and third dividend turns out 45 which is absurd and will not be dividable by 108]

(3) The third Gross Dividend is 1125. Subtract 3ab² (here, a=6, b=2, first two quotients) i.e. 3*6*2² = 72 from 1125 (i.e. 1125-72=1053) Therefore, Third Actual Dividend is 1053; divide 1053 by 108 gives 9 and 81 as Q and R.

(4) The fourth Gross Dividend is 818. Subtract 6abc + b³ (here, a=6, b=2, c=9) i.e. 6*6*2*9+2³ = 656 from 818 (i.e 818-656=162) So, Fourth Actual Dividend is 162. Divide this again by 108 and write down 0 and 162 as Q and R.

(5)  The fifth Gross Dividend is 1621. Subtract 3ac²+3b²c (here, a=6, b=2, c=9) i.e. 1458+108 = 1506 from 1621 (i.e 1621-1506=55) So, Fifth Actual Dividend is 55. Divide it by 108 and write down 0 and 55 as Q and R.

(6) The sixth Gross Dividend is 558. Subtract 3bc² (here, b=2, c=9) i.e. 486 from 558 (i.e 558-486=72) So, Sixth Actual Dividend is 72. Divide this by 108 and write down 0 and 72 as Q and R.

(7) The last / seventh Gross Dividend is 729. Subtract c³ (here, c=9) i.e. 729 from 729 (i.e 729-729=0) So, Seventh Actual Dividend is 0 and write down 0 and 0 as Q and R.

Put decimal after 3 digits (N=3). After decimal there are all zeros. This means that the given number is a perfect cube and the cube root is 629.
(After putting decimal, if there are still numbers except 0's than the number is not perfect cube)

Steps involved in finding dividend, quotient and reminder for (a+b+c+d)³ are:
(1) First determine D, Q and R
(2) From the second dividend, no deduction is to be made.
(3) From the third, subtract 3ab²
(4) From the fourth, deduct 6abc+b³
(5) from the fifth, subtract 6abd+3ac²+3b²c
(6) from the sixth, deduct 6acd+3bc²+3b²d
(7) from the seventh, subtract 6bcd+3ad²+c²
(8) From the eighth, subtract 3bd²+3c²d
(9) From the ninth, subtract 3cd²
(10) From the tenth, subtract d³; and so on.

OR We can convert (a+b+c+d) into (a+b+c). By considering first two groups into one group.
For example: 12278428443 can be written as
12, 278, 428, 443 (a+b+c+d)
12278, 428, 443   (a+b+c)
But, in second, we shall get the first quotient bigger.

Lets take one more example of an imperfect cube (not a perfect cube).
Find cube root of 417 upto 3-decimals place.

So, Cube root of 417 is 7.471

Hope these methods will help you all in computing cube root of the number.

In the upcoming articles, we will discuss about various techniques of division using Vedic Math.

Vedic Math - Cube Roots of more than 6-Digit Number - Part II

In last article, we have discussed the method to find cube root of more than 6-digit numbers; especially the odd numbers. Today we shall discuss the procedure for even numbers. In this procedure, only two extra steps are added, one in the beginning and other at the end. Rest all is same.

Procedure: As first added step, we keep on dividing the number by 8 till we get an odd cube. Following it, same method of successive elimination of the digits will apply. At the end, multiply the cube root by 8 to obtain the cube root of the original number.

Example :  2840362499528
First, we continue without using those two additional steps, which will help you to understand the problems arises while dealing with even cubes.

The cube root of the cube 2,840,362,499,528      (say, F + J + H + M + L )
Here,  N=5       (means that cube root will be of 5 digits number)
L=2                  (i.e. 2³=8, matching with the last digit of the last group '528')
and F=1            (i.e, 1³=1, nearest cube of first group '1')

Step1 : L=2 & L³=8. Subtracting this,              

Step2 : 3L²M=12M (substituting L = 2)
            Hence, 12M = Number ending with 2
    Here M is either '1' or '6'      (ambiguous values)
            Lets take 6  (pure gamble)
     
    Now, Deducting 3L²M = 12M = 72  

Step3 : 3LM²+3L²H = 12H + 216 (substituting L = 2, M = 6)
            12H + 216 = Number ending with 8
      12H = Number ending with 2                                    
            Here H is either '1' or '6'                                      
    Lets take 1 (again gamble)

    Now, Subtract 3LM²+3L²H = 12H + 216
                                                         = 228

Step4 : 3L²J+6LMH+M³ = 12J+12+216          
                                             = 12J+228
        12J+228 = Number ending with 6
12J = Number ending with 8
        Here J is either '4' or '9'
        Lets take J = 4  

Since we already know 'F' , so no need to know the expansion of (F+J+H+M+L)³ 
Therefore, cube root is 14162        (F=1, J=4, H=1, M=6, L=2)

In the above example, we see that there are so many ambiguous values like in step 2, 3, 4. To solve this problem, we divide the number by 8.
So,      

After first division by 8, if we get the last digit as odd number; we shall consider this number. If last digit is still even, we shall again divide by 8 till the last digit comes out to be an odd number. Remember one more thing, we will multiply the final output by 8 only once and not the number of times we divide it by the number (like, after dividing 3 times '792 994 249 216' by 8, we get '1 548 816 893', an odd number. Then we calculate the cube root of this odd number. Finally we shall multiply the cube root with 8 only once,
output*8 = Final Cube Root)

For, 355,045,312,441
 N=4,
 L=1     (1³=1)
 F=7     (7³=343 < 355)
 
Step1 : L=1 & L³=1. Subtracting this,              

Step2 : 3L²M=3M (substituting L = 1)
            3M = Number ending with 4
    So M should be 8        
     
  Now, Deducting 3L²M = 3M                  
                                              = 24      

Step3 : 3LM²+3L²H = 3H + 192 (substituting L = 1, M = 8)
           3H + 192 = Number ending with 2
  3H = Number ending with 0                
           Hence H = 0                      
                                                             
   Therefore, Cube Root is 7081    (F=7, H=0, M=8, L=1)

The Cube Root of the original number = 7081*8
                                                                = 14162 


In next article, we shall learn to find the cube root for all cube numbers (whether perfect or not). Thanks for visiting the blog. Please keep sharing the knowledge by posting in 'comments' section.

If you like the article, you may contribute by:

• Posting your comments which will add value to the article contents
• Posting the article link on Social Media using the Social Media Bookmark bar
• Connecting with 'VedantaTree' on Facebook (https://www.facebook.com/VedantaTree)

Vedic Math - Cube Roots of more than 6-Digit Number - Part I

Back after a long break. In previous article, we learn how to find the cube root of 4 or 5 or 6 digits perfect cubes. Let us continue it further and discuss how to find the cube root of perfect or imperfect cubes.

In this article, we shall learn to find the cube roots for:
1. Cube root of perfect cubes, for any number of digits.
2. Cube root for all the cubes, whether perfect cubes or not.

To summarize what we have learned till now for cube root:

Arrange the given number in three-digit groups, starting from right to left. A single digit, if any left over at the left hand side, is counted as a simple group itself. The number of  digits in the cube root will be the same as the number of digit-groups  in the given  number itself.

• 169 will count as 1 group 
• 1 258 will count as 2 groups 
• 43 781 will count as 2 groups
• 2 154 890 will count as 3 groups

If the given number has 'n' digits, its cube root will be having n/3 or (n+1)/3 digits. Also remember few other points from previous article:

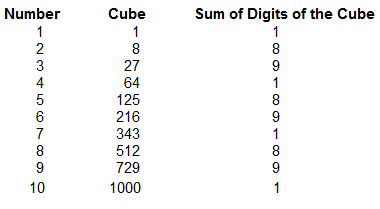
The Cubes  of the first nine natural numbers    
1³ = 1        2³ = 8        3³ =27        4³ = 64        5³ = 125        6³ = 216        7³ = 343        8³ = 512         9³ = 729        10³ = 1000
From it, we understand that

• 1,4,5,6,9,0 numbers repeat themselves in the ending of their cubes
• 2,3,7 and 8 have their complements from 10, at the end of their cube

Let us start with actual technique now. Any number can be written in an algebraic expression. For example, if arithmetical number is 'dcba', it can be written in algebraic form as:
Algebraic Expression is: a + 10b + l00c + 1000d.

Now if we need to find the cube of a number 'cba', algebraically we can expand it like  (a+10b+10²c)³. Let us expand it:
(a+10b+10²c) ³ =  a³ + 10 (3a²b) + 10² (3ab²+3a²c) + 10³ (b³+6abc) + 10⁴ (3ac²+3b²c) + 10⁵ (3bc²) + 10⁶ (c³)

Now removing the powers of ten and putting the result in algebraic form, it tells us the formation of cube as:
(1) The units' place is determined by a³.
(2) The tens' place is contributed by 3 a²b
(3) The hundreds' place is contributed to by 3ab² + 3a²c
(4) The thousands' place is formed by b³ + 6abc
(5) The ten thousands' place is given by 3ac² + 3b²c
(6) The hundred thousands' (lakhs') place is constituted of 3bc² ; and
(7) The millions' place is formed by c³.

The number of zeroes in the various coefficients of the expanded Algebraic Expression are the basis of the formula / analysis.

Case1 :  Cube root of perfect cubes for any number of digits

Suppose we have a cube number n of any number of digits. To find its cube root, find following:
- The number of groups (N) in cube (as we discussed above to make the sets of 3 digits)
- First digit of cube root denoted as 'F' (Nearest cube root of first group from left)
- Last digit of cube root denoted as 'L' (Cube root of last group from left)
- Middle numbers of cube root(i.e. 'M' or 'H' or 'J'....), we shall find using the procedure.

Following are the steps for the procedure:
(i) From the units' place of given number, subtract the L³ (i.e. a³, refer to algebraic expression above); and that eliminates the last digit of the number.
(ii) From the ten's place, we subtract 3L²M (i.e. 3a²b) and thus eliminate the second last digit (penultimate digit).
(iii) From the hundreds' place, we subtract 3LM² + 3L²F (i.e. 3ab² + 3a²c) and hence eliminate the pre-penultimate digit.
and so on

Let us understand it with an example.

Example 1 :  83453453

First arrange the numbers in groups i.e. 83,453,453
Here the number of 3 digit groups i.e. N = 3 (that also means that cube root will be of 3 digits number)
Last digit of the number is 3. The last digit of cube root of the number ending with 3 should be 7 (i.e.7³ = 343) So L = 7
The first group is 83 , the closest minimum exact cube to 83 is 64 which is nothing but 4³, therefore, F = 4

Hence N = 3, L = 7, and F = 4

And let us proceed to find the middle number:

Step1 : L=7 so L³=343                                                      
        Now subtract '343' from the last digit

       This eliminates the last digit of number, and give way to calculation of middle numbers

Step2 :   3L²M
= 147M        (substituting L = 7)
Now the last digit of 147M is '1' (which is the last digit of the number '8345311' after subtracting in first step).
            Hence,  147M = Number ending with 1
So M should be 3 ( because 147*3 can give a number ending with 1)
     
Deducting 3L²M = 147M = 147*3 = 441  

     

This eliminates the second last digit of number, and give way to calculation of further numbers.

Step3 :  3LM² + 3L²F = 147F + 189  =  ending with 7 (last digit of '834487' )
             147F  =  Number ending with 8   (i.e.834487-189)
        Hence, F = 4     (147*4 can give a number ending with 8)

 Hence, Cube Root = 437

Note:- The last step can be skipped safely, as we were already aware about the the first digit of cube root i.e. F.

Example 2: 13824
Arrange the number in groups i.e. 13, 824
Here N=2 (which means that cube root will be of 2 digits number)
L = 4 (i.e. 4³ = 64) and
F = 2 (exact cube near to 13 is 8 i.e.2³)
Therefore,  cube root = 24

Example 3 : 76928302277
Arrange the number in groups i.e. 76, 928, 302, 277  (say, F + H + M + L )
Here N = 4 (which means that cube root will be of 4 digits number, FHML)
L = 3 (i.e. 3³ = 27, matching with the last digit of the last group '277')
and F = 4 (i.e, 4³ = 64, nearest cube of first group '76')

Step1 : L=3 & L³=27. Subtracting this,    

Step2 : 3L²M=27M (substituting L = 3)
        Now the last digit of 27M is '5' (which is the last digit of the number '7692830225' after subtracting in first step).
        Hence, 27M = Number ending with 5
So M should be 5 ( because 27*5 can give a number ending with 5)      
     
Now, Deducting 3L²M = 27M                                    
                                   = 135         (27*5)        

Step3 : 3LM²+3L²H = 27H + 225 (substituting L = 3, M = 5)
            27H+225 = Number ending with 9
27H = Number ending with 4   (i.e.769283009-225)  

           Hence,  H = 2   (27*2 can give a number ending with 4)                          
So,  3LM²+3L²H = 27H+225 = 27*2+225 = 279            

Therefore, cube root is 4253    (F=4,  H=2,  M=5,  L=3)            

Note: According to the procedure, we can determine the first digit by the same method of successive elimination of the digits. For this, we have to expand (F + H + M + L)³. And, on expanding, we find that in the 4th step i.e. thousand's place number, 'F' appears to be '3L²F + 6LMH + M³'. We need to deduct this value to eliminate the fourth digit. So,

        3L²F + 6LMH + M³ = 27F+180+125          
                                         = 27F+305
        27F + 305 = Number ending with 3
27F = Number ending with 7
        Hence,   F = 4
        Therefore,  Cube Root = 4253  

[For reference, (10³d+10²c+10b+a) ³ = a³ + 10 (3a²b) + 10² (3ab²+3a²c) + 10³ (b³+6abc+3a²d) + 10⁴ (3ac²+3b²c+6abd) + 10⁵ (3bc²+3b²d+6acd) + 10⁶ (c³+3ad²+6bcd) + 10⁷ (3bd²+3c²d) + 10⁸ (3cd²) + 10⁹ (d³)]           

Note:- Again, in case of perfect cubes, the last step can be skipped safely, as we are already aware about the the first digit of cube root i.e. F.

Important point to notice is that above method can be applied for odd cubes only. If the cube is even, then we would found ambiguous values at each step; like we may get two possibilities of M, H,.... We shall discuss the procedure to find cube root of such even cubes in next article. Till then, practice above procedure and keep posting your queries and share any findings.

------------------------------------------------------------------------------------------------------------
If you like the article, you may contribute by:

• Posting your comments which will add value to the article contents
• Posting the article link on Social Media using the Social Media Bookmark bar
• Connecting with 'VedantaTree' on Facebook (https://www.facebook.com/VedantaTree)