In the last article, we discussed division by 9. And in this article, we discuss divisors below base value 10, 100 etc. In these, we do the pairing from right.
Easy way to divide by 9 can be extended for 8, 7 etc.
ab divided by m
The rule we use is:
1) Put a and b in the first row
2) Write a as quotient in third row
3) List p x a (a the quotient) in the second column of the second row. (p= 10 - m)
a | b
| p x a
----------
a | b +(p x a)
Quotient: a, remainder: b + (p x a)
Clearly this is easiest for 9, p= 10 - 9= 1
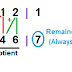
8) 3 | 1 7) 2 | 0 6) 1 | 1
| 6 | 6 | 4
--------- ---------- ----------
3 | 7 2 | 6 1 | 5
In the above examples with divisor 8, 7, and 6, we get quotient 3 reminder 7 , quotient 2 reminder 6 and quotient 1 reminder 5 respectively.
We have to multiply the quotient by 2 in the case of 8, by 3 in the case of 7, by 4 in the case of 6 and so on. What this means, that we have to multiply the quotient-digit by the Divisor's complement from 10.
For example, Divide 31 by 8
Step 1: We bring the first digit 3 into the answer as quotient.
Step 2: Then instead of adding this to the 1 as we do when dividing by 9, we add double of 3
(i.e. 3 * (10-8)) to the 1 and get 7 for the remainder.
We double the 3 because 8 is 2 below 10.
Lets extend it for three digits Dividend
abc divide by m, p=10-m
a | b | c
| p x a | p x ((p x a) + b)
--------------------------------------
Quotient: a / (p x a) + b, Remainder: (p x ((p x a) + b)) + c
Similarly, for 311 divided by 8
8) 3 | 1 | 1
| 6
--------------
3 | 7 | 14
--------------
37 | 15
---------------
38 | 7
Easy way to divide by 9 can be extended for 8, 7 etc.
ab divided by m
The rule we use is:
1) Put a and b in the first row
2) Write a as quotient in third row
3) List p x a (a the quotient) in the second column of the second row. (p= 10 - m)
a | b
| p x a
----------
a | b +(p x a)
Quotient: a, remainder: b + (p x a)
Clearly this is easiest for 9, p= 10 - 9= 1
8) 3 | 1 7) 2 | 0 6) 1 | 1
| 6 | 6 | 4
--------- ---------- ----------
3 | 7 2 | 6 1 | 5
In the above examples with divisor 8, 7, and 6, we get quotient 3 reminder 7 , quotient 2 reminder 6 and quotient 1 reminder 5 respectively.
We have to multiply the quotient by 2 in the case of 8, by 3 in the case of 7, by 4 in the case of 6 and so on. What this means, that we have to multiply the quotient-digit by the Divisor's complement from 10.
For example, Divide 31 by 8
Step 1: We bring the first digit 3 into the answer as quotient.
Step 2: Then instead of adding this to the 1 as we do when dividing by 9, we add double of 3
(i.e. 3 * (10-8)) to the 1 and get 7 for the remainder.
We double the 3 because 8 is 2 below 10.
Lets extend it for three digits Dividend
abc divide by m, p=10-m
a | b | c
| p x a | p x ((p x a) + b)
--------------------------------------
Quotient: a / (p x a) + b, Remainder: (p x ((p x a) + b)) + c
Similarly, for 311 divided by 8
8) 3 | 1 | 1
| 6
--------------
3 | 7 | 14
--------------
37 | 15
---------------
38 | 7
- We bring down the first digit i.e. 3,
- Add 2 x 3 (i.e. p x a) to 1 (i.e. b) in the next column and put down 7 (i.e.(p x a) + b),
- Then add 2 x 7 (i.e. p x ((p x a) + b)) to the 1 in the last column and put down 15 as the remainder.
- Since this remainder is bigger than 8, hence we compute answer further. As 15 > 8, so add 1 to quotient and subtract 8 from remainder. Final answer is quotient = 38 and reminder = 7