Vedic Math - Multiplication of numbers whose last digits add to 10 and first digits are same and vice-versa.

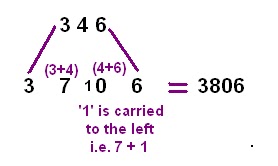
We had discussed this method in our previous articles for 2-digit numbers and today we shall explain the same method for 3-digit numbers.

A. Numbers whose last digits add to 10 and the remaining first digits are the same
Case 1: When sum of last two digits number is 100 
Example: 392 x 308
Here we can see that right digits sum is 100 i.e.(92 + 8) and left side digits are same. Here we can now apply the same method, which we discussed earlier for 2-digit number. But this time we must expect to have four figures on the right-hand side.

• First, multiply the right side numbers(92 x 08) and the result is 0736.
• Second, multiply 3 by the number that follows it, i.e.4, so the result of (3 x 4) is 12.
• And now the final output is 120736.

Example: 795 x 705
Here 95 + 05 = 100 and left side digits are same i.e. '7'. Hence it qualifies for this case.
In calculation, we shall multiple the last two digits and the left digit i.e. '7; with its next number '8'. So the calculation is:
795 x 705 = 7 x 8 | 95 x 05
                 = 56 | 0475
                 = 560475

Example: 866 X 834
Here 66 + 34 = 100 and left side digit is 8 and its next number is 9. So the calculation is:
848 x 852 = 8 x 9 | 66 x 34            (Note: For 66 x 34, we shall discuss in our upcoming articles)
                 = 72 | 2244
                 = 722244
         
         
Case 2: When sum of whose last digits is 10  and the remaining first digits are the same   
Example: 241 x 249
Here we can see that right digits sum is 10 i.e.(9 + 1) and left side digits are same i.e. 24. So we can now apply the same method as described above.
241 x 249 = 24 x 25 | 1 x 9
                 = 0600 | 09
                 = 60009

444 x 446 = 44 x 45 | 4 x 6
                 = 1980 | 24
                 = 198025
         
147 x 143 = 14 x 15 | 7 x 3
                 = 0210 | 21
                 = 21021

Special cases:
Case 1: Where numbers are not qualified for above case in general, but can be qualified after converting their form. Example is given below.

For example: 93 x 39
93 × 39 doesn't seems to comes under this method. But if we convert 93 to (3 × 31), then 31 × 39 comes under this method. So the calculation is
93 x 39 = 3 x 31 x 39
             = 3 x (31 x 39)
31 × 39 = 1209            (by same method discussed above i.e. 31 x 39 = (3 x 4) | (1 x 9) = 12 | 09 = 1209)
93 × 39 = 3 x 1209
             = 3627
         
The point to notice in the above example is that '39' needs '31' to qualify for method, and then we found that 93 is '3 × 31'.


Case 2: If the left hand digits are the same, but last digit's sum is not 10. We can still apply the same method that we discussed just above. For example: 35 x 37

In 35 x 37, both left hand numbers are 3, but 5 + 7 = 12 which is greater than 10. We can solve this in two ways.

First, we modify the numbers in such a way that we can apply the method used for "squaring numbers ending in 5":
35 x 37 = 35 x (35 + 2)
        = (35 x 35) + (35 x 2)   
        = 1225 + 70           (Take 35 x 35 = 3 x 4 | 5 x 5 = 12 | 25 = 1225)
        = 1295

Second approach is, we modify the numbers in such a way that we can apply the method discussed above. So we split 35 as 33 + 2. And observe that (33 x 37) comes under the above discussed method.
So, we rewrite it as:
35 x 37 = (33 + 2) x 37
        = (33 x 37) + (2 x 37)
        = 1221 + 74           (Take 33 x 37 = (3 x 4) | (3 x 7) = 12 | 21 = 1221)
        = 1295

One more example:
114 x 117 = 114 x (116 + 1)
          = (114 x 116) + (114 x 1)
          = 13224 + 114       (Take 114 x 116 = (11 x 12) | (4 x 6) = 132 | 24 = 13224)         
          = 13338
OR
114 x 117 = (111 + 3) x 117   (Rest of the procedure is same)

Now, take one more example where first digit remains same but addition of last digits is less than 10.
68 x 61 = 68 x (62 - 1)
        = (68 x 62) - (68 x 1)  (Rest of the procedure is same)
OR
68 x 61 = (69 - 1) x 61
        = (69 x 61) - (61 x 1)    (Rest of the procedure is same)   

B.Numbers whose last digits are same and first digits add to 10

Now let us solve some case where last figures are the same and the first figures add up to 10. This comes under the Vedic formula "The First by the First and the Last by the Last". For example: 47 x 67
Here we can see that left hand digits sum is 10 i.e.(4 + 6) and right hand digits are same i.e. 7 . So we can now apply the following method.

• Multiply the first digit of each number together i.e.(4 x 6 = 24). Add the last figure (7) into it (24 + 7 = 31) which is the first part of the answer.
• Multiplying the last figures together(i.e.7 × 7 = 49) which is the last part of the answer.
• The final answer is 3149.

Let us take some more examples

34 x 74 = (3 x 7) + 4 | 4 x 4
        = 21 + 4 | 16
        = 2516

98 x 18 = (9 x 1) + 8 | 8 x 8
        = 9 + 8 | 64
        = 1764
       
23 x 83 = (2 x 8) + 3 | 3 x 3
        = 16 + 3 | 09
        = 1909   

Note: You can do "Squaring of numbers between 50 and 60" with the same method. You might be thinking that how this could be. But see, left hand digits sum is 10 i.e.(5 + 5) and right hand digits are same. So we can now apply the same method. We had already discussed it in "squaring numbers near 50", both are almost same but different presentation. See the following example:

58²= 58 x 58
     = (5 x 5) + 8 | 8 x 8
     = 25 + 8 | 64
     = 3364
   
53²= 53 x 53
     = (5 x 5) + 3 | 3 x 3
     = 25 + 3 | 09
     = 2809
   

How do you like these Vedic Maths technique, please let us know.

Vedic Math - Multiplication of numbers with a series of 1's

In the previous article, we learnt the technique of "how to multiply numbers with a series of 9’s". In this article, we shall learn the technique of "how to multiply numbers with a series of 1’s". So, we shall multiply the numbers with 1, 11, 111,..... etc.

I. Let us start with the vedic multiplication by 11

In this technique, we use "vertically and crosswise" vedic sutra. Take example of ab x uv, and apply the sutra as follows:

       a         b
       u         v
   ---------------------
   a x u | av + ub | b x v
   ---------------------

(Here '|'  is used just as separator)

Here we are splitting the answer in three parts as following:

• vertically                         =(b x v)
• crosswise multiplication and add   =(a x v) + (b x u)
• vertically                         =(a x u)

During multplication with 11, u=1 and v=1, means:

           a               b
           1               1
         --------------------
           a  |  a + b  |  b
         --------------------


Example:  Multiply 53 by 11

Here one point to consider is that we should write the answer from right to left. Because, in case, sum of the digits of multiplicand comes in 2 digits, we need to carry the ten's place digit to next (left side) calculation. You will notice it in next examples.

Example:  Multiply 68 by 11

Step 1 : Last part of the answer is same as the last part of the multiplicand i.e. 8 (8 x 1). > 8
Step 2 : For middle part, sum the digits of multiplicand i.e. 6 + 8 = 14. We will not write '14' as the middle  part. We write down '4' and digit '1' is carried over. > 4
Step 3 : First part is now, first digit of multiplicand i.e. 6. But we have one digit as carry from step 2, so we shall add this to first part. Now first part will become 6 + 1 = 7. > 7

Finally, answer is 748.

Some examples are given below:
54 x 11= 5 | 9 | 4 = 594
35 x 11= 3 | 8 | 5 = 385
81 x 11= 8 | 9 | 1 = 891
96 x 11= 9 | 15 | 6 = 10 | 5 | 6 = 1023 ( here '1' carry over)
88 x 11= 8 | 16 | 8 = 9 | 6 | 8 = 968   (again '1' carry over)


This technique is also applicable to numbers having more than 2 digits. You just need to take first and last digits of multiplicand as it is (as done in previous examples), and continue adding the adjacent two numbers for middle parts (more than one parts now).

Example: Multiply 346 by 11

Following examples will help to understand more.

267 x 11   = 2 | 2+6 | 6+7 | 7          
                =  2 | 8 | 13 | 7       
                = 2 | 9 | 3 | 7      
                = 2937                   
        
2678 x 11  = 2 | 2+6 | 6+7 | 7+8 | 8   
                 =  2 | 8 | 13 | 15 | 8  
                 = 2 | 9 | 4 | 5 | 8  
                 = 29458    

26789 x 11 = 2 | 2+6 | 6+7 | 7+8 | 8+9 | 9
                  =  2 | 8 | 13 | 15 | 17 | 9
                  = 2 | 9 | 4 | 6 | 7 | 9
                  = 294679 


II. Now, let us learn to multiply any number with 111.

In this, since multiplier is 3-digit number, so for middle part, we shall start by adding first two digits and then keep on adding next three ( and next three and so on) and then will end by adding the last two digits. First and last part will be same as described above. You will understand this with following examples.

Examples:

365 x 111    = 3 | 3+6 | 3+6+5 | 6+5 | 5          
                   = 3 | 9 | 14 | 11 | 5              
                   = 40515

3645 x 111   = 3 | 3+6 | 3+6+4 | 6+4+5 | 4+5 | 5        
                    = 3 | 9 | 13 | 15 | 9 | 5             
                    = 404595 

567894 x 111  = 5 | 5+6 | 5+6+7 | 6+7+8 | 7+8+9 | 8+9+4 | 9+4 | 4
                       = 5 | 11 | 18 | 21 | 24 | 21 | 13 | 4                    
                       =   63036234

57 x 111     = 057 x 111    
                  = 0 | 0+5 | 0+5+7 | 5+7 | 7      
                  = 0 | 5 | 12 | 12 | 7   
                  = 06327 = 6327  


III. Similarly, we can multiple any number by 1111.

In this, since multiplier is 4-digit number, so for middle part, we shall start by adding first two digits, then first three digits and then keep on adding next four ( and next four and so on) and then will end by adding the last three digits, and then last two digits. First and last part will be same as described above. You will understand this with following examples.

Examples:

5678 x 1111   = 5 | 5+6 | 5+6+7 | 5+6+7+8 | 6+7+8 | 7+8 | 8          
                      = 5 | 11 | 18 | 26 | 21 | 15 | 8          
                      = 6308258

126453 x 1111 = 1 | 1+2 | 1+2+6 | 1+2+6+4 | 2+6+4+5 | 6+4+5+3 | 4+5+3 | 5+3 | 3
                        = 1 | 3 | 9 | 13 | 17 | 18 | 12 | 8 | 3   
                        = 140489283

43 x 1111         = 0043 x 1111     
                        = 0 | 0+0 | 0+0+4 | 0+0+4+3 | 0+4+3 | 4+3 | 3                              
                        = 0 | 0 | 4 | 7 | 7 | 7 | 3                       
                        = 47773

Using the same method, we can multiply any number by a series of 1’s. If you want to multiply a number by 11111 (irrespective of how big is the multiplicand), the only difference will be that we will add maximum five numbers at a time for middle part of answer(because there are five ones in 11111).

And remember the basic rule that we use in normal addition — carry over the digit to its left when you have a two-digit answer.

Vedic Math - Multiplication of numbers with a series of 9’s

Another special case of multiplication is, multiplication with numbers like 9, or 99, or 999, or 9999.....so on. It feels like if multiplier is a big number, the calculation will be tough. But, with the help of vedic math formulae, the multiplication is much easier for all '9' digits multiplier. By using the method given below, we can multiply any number with 99,999,9999, etc. very quickly.

Please note that the methods or the vedic formulae, that we use in this calculation, are "By one less than the one before"  and "All from 9 and the last from 10".

There are three cases for the multiplication of numbers with a series of 9's.

• Case 1: Multiplying a number with a multiplier having equal number of 9’s digits                                              (like 587 x 999)
• Case 2: Multiplying a number with a multiplier having more number of 9’s digits                                             (like 4678 x 999999)
• Case 3: Multiplying a number with a multiplier having lesser number of 9’s digits                                             (like 1628 x 99)

The method to solve 'Case 1' and 'Case 2' is the same, but for 'Case 3', the method is different. Let us start with 'Case 1'.

Case 1: Multiplying a number with a multiplier having equal number of 9’s digits

Multiply 587 by 999

           587
       x  999
       ------------
        586 413
       
Solution is,

•  Let us first do the calculation by conventional method to understand the solution. Result will be 586413.
• Split the answer in two parts i.e. '586' and '413'.
• Let's see the first part of the result, i.e. 586. It is reduced by 1 from the number being multiplied i.e. 587 - 1 = 586. {Vedic sutra "By one less than the one before"}
• Now see the last part, i.e. 413. Subtract the multiplicand i.e. 587 from 1000 (multiplier + 1). Vedic Sutra applied here is "All from 9 and the last from 10", and hence we substract 587 from 1000. So the outcome will be (9 -5 = 4, 9 - 8 = 1, 10 - 7 = 3) , and result is 413. Refer to image below for more clarity:

Case 2: Multiplying a number with a multiplier having more number of 9’s digits
Multiply 4678 by 999999

           4678
     x   999999
   ----------------
    4677 995322   

Here, 4678 is 4-digit number and 999999 is 6-digit number. So, we can rewrite 4678 as 004678 to make 6-digit number. Now, it turns out to be same as case 1. So, same method is going to be applied.

The result has two parts:

• The first part of the result, i.e. 4677, which is reduced by 1 from the number being multiplied      (4678 - 1). {Vedic sutra "By one less than the one before"}
• For the last part of answer (995322), Subtract the multiplicand i.e. 004678 from 1000000   (1000000 - 004678). Here we are applying the vedic formula "All from 9 and the last from 10" on 004678. Calculation is like:

•  9 - 0  =9
•  9 - 0  =9
•  9 - 4  =5
•  9 - 6  =3
•  9 - 7  =2
• 10 - 8 =2

• So the result is 995322
• Now combine first and last part, and you get the final answer i.e. '4677995322'

Case 3: Multiplying a number with a multiplier having lesser number of 9’s digits

Multiply 1628 by 99

For this case, method is changed. In this, we rewrite 1628 x 99 as 1628 x (100 - 1). So,

                     1628(100 - 1)
                   = 162800 - 1628
                   = 161172

Here, calculation might get slow during substraction. But once you learn the vedic subtraction, it will become fast. In coming sessions, we shall discuss it.

OR  there is another approach given below, by spliting the solution in three parts.

                1628 x 99 = 16 : 11 : 72

Now, see how we get this result using Vedic Math:

                        16     : 28    : 100
                                 : 17    :   28
                      -----------------------  
                        16     : 11     :  72

                                                                                          
Steps to follow are given below:

• Split the multiplicand in such a way that the right hand side number contains the digits equal to the number of digits in multiplier. Like here, multiplier is 99 (having 2 digits). So after splitting the multiplicand, the right hand side number will be 28. Now, there are two parts of multiplicand after split i.e. 16 and 28.
• Create three different virtual columns, and place two parts of splited number in first and second column.
• In third column, put (multiplier + 1) i.e. 100 in this case
• Now add '1' to first part of multiplicand, and place it in middle column of second row. Number of digits should be equal to number existed in first row in same column. If it is not, shift the extra digits in first column of second row.
• Place second part of multiplicand (28, from first row) in third column.
• Now subtract numbers in second row from first row numbers, in their respective columns. In case of middle column, if first row number is lesser than second row number, we can borrow '1' from first column value.
• If we follow this, the answer for each column will be
• Third Column: 100 - 28 = 72
• Second Column: 28 -17 = 11
• First Column: 16 - 0 = 16
• So the answer is, '16 11 72'

Example where number in middle column of first row is lesser than second row value (63 x 9):
                6    : 3    :  _
                _    : 7    :  3
               -----------------
                5    : 6    : 7

Here, 3 is less than 7 and subtraction is not possible. Hence we borrow '1' from first column value i.e. borrow 1 from 6 and 3 becomes 13 and left part is now 5.

One more example to make it more clear: 17119 x 99

                       171   : 19   : _ _
                           1   : 72   :  19
                    ----------------------   
                       169   : 47   : 81


Here, don't get confuse by seeing '1' in the first column of second row. It is just taken from '172' (which is one more than '171'). As per the method, middle column should have number having digits equal to multiplier. So we shift '1' to first column. Rest all is same.

Hope you understandand this method. If you have any question, please post in comments. In the next session, we shall discuss about multiplication of numbers with a series of 1's.

Vedic Math - Squaring of numbers near '50'

In this article, we pick another special case of squaring i.e. squaring numbers which are near 50. It can have two cases, which are:

• Case 1: Numbers greater than 50.
• Case 2: Numbers lesser than 50

In both the cases, we need to take 50 as the base value. First let us take 'Case 1' i.e. 'Numbers greater than 50'.

Case 1 -
Take an example: Say, 54²=2916 
Consider this answer in two parts: 29 (first part) and 16(second part). Now let us study, how Vedic Math can help us to achieve this answers or both of these parts.

As we are taking '50' as base, so the number presentation will be like 50 + 4. So the first part is 50, and second part is 4.

For the first part of the answer:

1. Pick the first part i.e. 50.
2. Pick the first digit i.e. 5
3. Square this digit i.e. 5² > 25
4. Add 4(second part) to it
5. And we get our first part of the answer i.e. 29 (25 + 4).

For the second part of answer, following are the steps:

1. Pick second part i.e. 4
2. Square this digit i.e. 4² > 16
3. And we get our second part of the answer i.e. 16

So the answer is 2916

Let us understand it with another example to make it more clear. Say, 61²=3721
As we are taking '50' as base, so the number presentation will be like 50 + 11. So the first part is 50, and second part is 11.

For the first part of the answer:

1. Pick the first part i.e. 50.
2. Pick the first digit i.e. 5
3. Square this digit i.e. 5² > 25
4. Add 11(second part) to it
5. And we get our first part i.e. 36 (25 + 11).

For the second part of answer, following are the steps:

1. Pick second part i.e. 11
2. Square this digit i.e. 11² > 121
3. Now the result is of three digit. So the first digit (1) will be added to the first part i.e. 1 + 36 = 37
4. So first part becomes 37 now
5. And second part of answer will be 21 

So the answer is 3721. Refer to image below for visual representation.

Now, let us study 'Case 2' i.e. Numbers lesser than 50.

Case 2 -
Take an example: Say, 48²=2304
As we are taking '50' as base, so the number presentation will be like 50 - 2. So the first part is 50, and second part is (-2). For numbers below 50, we take the deficiency from 50 (2 in this case), to get the number (48 in this case); and use the square of the deficiency (2²= 4 in this case) for calculation.

For the first part of the answer:

1. Pick the first part i.e. 50.
2. Pick the first digit i.e. 5
3. Square this digit i.e. 5² > 25
4. Add (-2) (i.e. second part) to'25'
5. And we get our first part i.e. 23 (25 + (-2)).

For the second part of answer, following are the steps:

1. Pick second part i.e. (-2)
2. Square this digit i.e. (-2)²  =  4
3. And second part of answer will be 04

So the answer is 2304. Refer to image below for visual representation.

In the second case, we explore the sub-sutra "Whatever the deficiency lessen by that amount and set up the square of the deficiency"

The Algebra behind this method is:

• (50 + a)² = 100 (25 + a) + a²   (if number is above 50)
• (50 - a)² = 100 (25 - a) + a²    (if number is below 50)

Here are few exercises for your practice:

43² = ?

49² = ?

56² = ?

52² = ?

62² = ?


Try it. I hope by now you would have understood the method. Even then if you have any difficulty, post your doubts here. Enjoy!!

Please do share your views that would be having great value for us and will encourage us.

Vedic Math - Squaring Of Numbers Ending with '5'

In this article, we shall discuss a very common and interesting trick to square those numbers quickly which are having '5' as last digit. For example, what is the result of 65², 85², 125² ?

Let us start with an example:- 35 x 35. How will you multiply?

The conventional approach is-

     35
   x 35
   -------
    175
   105
 --------
   1225
 --------
 In above problem, we followed the following steps:

1. In first step, we multiply 5 by 35, get 175 and wrote it below the line.
2. In second step, we multiply 3 by 35, get 105, wrote it below the first step and leave one space from right.
3. In last, we add results from both the steps and get 1225 as answer.

Now here is the magical trick or quicker way to do this calculation using Vedic Math (to square any number with a 5 on the end). Let us have a look on the same example once again, following 'Vedic Math' steps to solve it.

1. In 35, the last digit is 5 and other number is 3.
2. Add 1 to the top left digit 3 to make it 4 (i.e. 3+1=4) (See the image below).
3. Then multiply original number '3' with increased number i.e. '4'. Like 3 x 4, and we get 12.
4. Now you can see that this is the left hand side of the answer.
5. Next, we multiply the last digits, i.e 5 x 5 and write down 25 to the right of 12.
6. And here we come up with a desired answer, 1225
7. Visual representation is given below.

 Let us do one more exercise. Find the square of 105:
 
    105
  x 105
   -------
   11025
   -------

I'm going to explain the magical trick method once more.

1. In 105, the number apart from 5 the digits are 1 and 0, that is, 10
2. Add 1 to the top left digit 10 to make it 11(i.e. 10+1=11).
3. Multiply the original left hand side number with its successor number i.e. 10x11, and we get 110.
4. Write this on the left hand side.
5. Multiply the last digits, i.e 5 x 5 and write down 25 to the right of 110.
6. And here is the answer > 11025

So you can see how easy it is to square the numbers which are ending with a 'five' (5) digit! In fact, if you memorize this technique and practice it, eventually you would be able to perform these calculations verbally (in mind). Just multiply the non-five number (left side number) with its successor number and put outcome on the left side. Multiply the last digits (5 x 5) and put 25 on right side of the previous multiplication.

A few more examples/exercises are given below:

25² = 625

45² = 2025

65² = 4225

95² = 9025

115² = 13225  (11 x 12 = 132)

You try the above examples and I'm sure that you will solve these problems fast or might be orally.

The technique of squaring numbers ending with 5 is a very popular technique. With this technique, you have used the formula (sutra) "By One More Than the One Before" , which provides a beautiful and simple way of squaring numbers that end by 5.

The ALGEBRA behind this method is (ax+5)²= a(a+1)x² + 25, where x=10. 

Now here the question arises in your mind that: Is this formula applicable to a number that ends with 5 only?
Answer: It is not applicable to all kind of multiplications. But you will be happy to know that the above formula can be applied to the multiplication of numbers whose last digits add to 10 and the remaining first digits are the same. But remember, same rule is not applied on the vice-versa i.e. if last figures are the same and the first figures add up to 10. See the image below.



So same rule is applicable for case 1, but not for case 2.

We will take one more example of the same kind.
     6 9
   x 6 1
    --------
    42 09
    --------
Here we can see that right digits sum is 10 i.e.(9+1) and left side digits are same. So we can now apply the same method.

1. First, multiply the right side numbers(1 x 9) and the result is 09.
2. Second, multiply 6 by the number that follows it, i.e.7, so the result of (6 x 7) is 42.
3. And now the final output is 4209.

Now, following are some of the problems for your practice.

1. 76 x 74
2. 33 x 37
3. 91 x 99
4. 85 x 85
5. 55 x 55

So this is all for today. Hope you have enjoyed the 'Vedic Math' tricks. We shall come up with more tricks soon.

What is Vedic Math?

We are going to start a new and very interesting section and that is 'VEDIC MATH'. Many of us are interested in increasing our productivity with calculations. This is where ‘Vedic Math’ helps us. It teaches us many ways to do the calculations quickly and if practiced correctly then all the calculations can be done in mind. Hence it helps us not only in our work, but routine works also. Vedic Math is also very useful for students to get rid of math phobia and improve grades. With these techniques one could be able to solve the mathematical problems 15 times faster. It improves mental calculations, concentration and confidence. Isn’t this great!

Once you are aware of the basics of Vedic Math, you can practice and make yourself a human calculator. Vedic Mathematics is magical. Let us take a simple example of multiplication to feel what Vedic Math is and what it can do.

So, let’s try 14 times 11.

•     Split the 14 apart, like:
•     1    4
•     Add these two digits together
•     1 + 4 = 5
•     Place the result, 5 in between the 14 to have 154
•     And the result is
•     14 X 11 = 154

This is a very basic example to show the magical power of Vedic Math. Once you learned all the techniques, you will be able to do various complex calculations very fast as mentioned above. Before we proceed towards the different techniques of Vedic mathematics in detail, we first give you brief background of Vedic Mathematics history.

'Vedic Mathematics' is the name given to the ancient system of mathematics derived from ancient treasure of knowledge called ‘Veda’. ‘Veda’ means knowledge. Vedic Mathematics believes to be a part of ‘Atharva Veda’. It a unique technique of calculations based on simple rules and principles, using which any mathematical problem related to arithmetic, algebra, geometry or trigonometry can be solved quickly and possibly orally (once you master it).

Vedic Mathematics was devised probably thousands of years back; however it was rediscovered again from the Vedas between 1911 and 1918 by Sri Bharati Krsna Tirthaji (1884-1960). According to his research all of mathematics is based on sixteen Sutras or word-formulae. For example, 'Vertically and Crosswise` is one of these Sutras. These formulae describe the way the mind naturally works and are therefore a great help in solving the problems.

Following are 16 Sutras and 14 Sub-Sutras:

Sutras (Formulae)

• By one more than the one before
• All from 9 and the last from 10
• Vertically and crosswise
• Transpose and apply
• If the Samuccaya (i.e. both sides of the equation) is the same it is zero
• If one is in ratio the other is zero
• By addition and by subtraction
• By the completion or non-completion
• Differential calculus
• By the deficiency
• Specific and general
• The remainders by the last digit
• The ultimate and twice the penultimate
• By one less than the one before
• The product of the sum
• All the multipliers

    Sub-Sutras (Sub-Formulae)

• Proportionately
• The remainder remains constant
• The first by the first and the last by the last
• For 7 the multiplicand is 143
• By osculation
• Lessen by the deficiency
• Whatever the deficiency lessen by that amount and set up the square of the deficiency
• Last totaling 10
• Only the last terms
• The sum of the products
• By alternative elimination and retention
• By mere observation
• The product of the sum is the sum of the products
• On the flag

-Excerpt from Sri Bharati Krsna Tirthaji's "Vedic Mathematics"

We will discuss these sutras and subsutras in greater detail later. First we will go with some of the tips and tricks on addition, subtraction, multiplication and division. And side by side, you realize that eventually we shall come across these sutras in different aspects of mathematical calculations, as all those calculations utilize these sutras (formulae) in one form or other. Then you shall also learn and understand the meaning of these sutras.

A simple example,

If we wished to subtract 378 from 1,000; we simply apply the sutra "all from nine and the last from 10". Each figure in 378 is subtracted from 9 and the last figure is subtracted from 10, yielding 622.

1000  -  378      =    622

1000  -     3                  7                8
            subtract    subtract    subtract
            from 9       from 9       from 10
               |                |                  |
               6               2                 2   

Vedic Mathematics is quite simple in calculations, and that means you can do simple to complex calculations orally. Imagine how much value that can add to different procedures in day to day life. Further, this whole system was devised considering utmost flexibility and extensibility. Pupils were encouraged to learn from practiced techniques and devised their new techniques. It is quite beautiful approach to mathematics. However, you can appreciate this beauty only by practicing it yourselves.

So, we shall start learning more about Vedic Math with coming articles. I hope you had a great time while reading brief history and few basic concept of Vedic Math. And wish, you will enjoy more with coming sessions. Then the phobia of math will disappear as you move forward with reading and eventually it fills you with lots of confidence. I’ll come up with more and more information soon.

Do you know:- 
What is the name of Veda, from which Vedic Mathematics comes from?